Examining the causal structures of deep neural networks using information theory

Deep Neural Networks (DNNs) are often examined at the level of their response to input, such as analyzing the mutual information between nodes and data sets. Yet DNNs can also be examined at the level of causation, exploring "what does what" within the layers of the network itself. Historically, analyzing the causal structure of DNNs has received less attention than understanding their responses to input. Yet definitionally, generalizability must be a function of a DNN's causal structure since it reflects how the DNN responds to unseen or even not-yet-defined future inputs. Here, we introduce a suite of metrics based on information theory to quantify and track changes in the causal structure of DNNs during training. Specifically, we introduce the effective information (EI) of a feedforward DNN, which is the mutual information between layer input and output following a maximum-entropy perturbation. The EI can be used to assess the degree of causal influence nodes and edges have over their downstream targets in each layer. We show that the EI can be further decomposed in order to examine the sensitivity of a layer (measured by how well edges transmit perturbations) and the degeneracy of a layer (measured by how edge overlap interferes with transmission), along with estimates of the amount of integrated information of a layer. Together, these properties define where each layer lies in the "causal plane" which can be used to visualize how layer connectivity becomes more sensitive or degenerate over time, and how integration changes during training, revealing how the layer-by-layer causal structure differentiates. These results may help in understanding the generalization capabilities of DNNs and provide foundational tools for making DNNs both more generalizable and more explainable.

What caused what? An irreducible account of actual causation

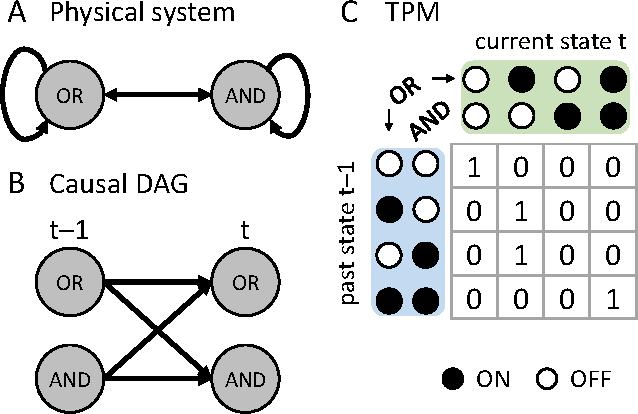
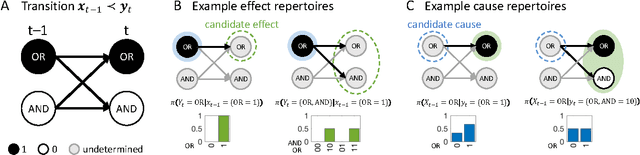
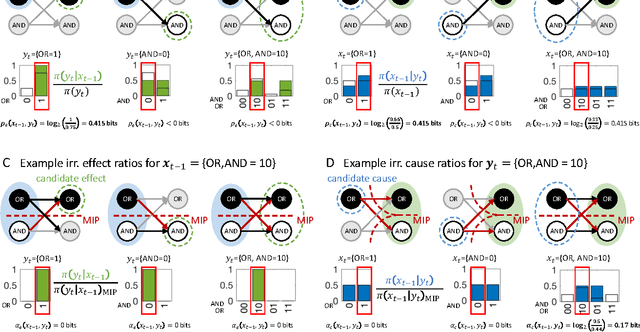
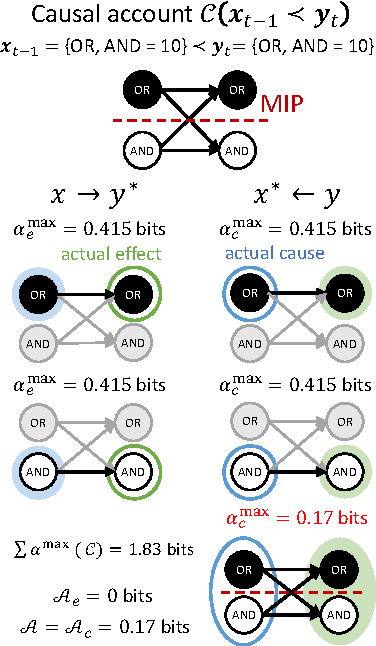
Actual causation is concerned with the question "what caused what?". Consider a transition between two subsequent observations within a system of elements. Even under perfect knowledge of the system, a straightforward answer to this question may not be available. Counterfactual accounts of actual causation based on graphical models, paired with system interventions, have demonstrated initial success in addressing specific problem cases. We present a formal account of actual causation, applicable to discrete dynamical systems of interacting elements, that considers all counterfactual states of a state transition from t-1 to t. Within such a transition, causal links are considered from two complementary points of view: we can ask if any occurrence at time t has an actual cause at t-1, but also if any occurrence at time t-1 has an actual effect at t. We address the problem of identifying such actual causes and actual effects in a principled manner by starting from a set of basic requirements for causation (existence, composition, information, integration, and exclusion). We present a formal framework to implement these requirements based on system manipulations and partitions. This framework is used to provide a complete causal account of the transition by identifying and quantifying the strength of all actual causes and effects linking two occurrences. Finally, we examine several exemplary cases and paradoxes of causation and show that they can be illuminated by the proposed framework for quantifying actual causation.