A Contrastive Symmetric Forward-Forward Algorithm (SFFA) for Continual Learning Tasks

The so-called Forward-Forward Algorithm (FFA) has recently gained momentum as an alternative to the conventional back-propagation algorithm for neural network learning, yielding competitive performance across various modeling tasks. By replacing the backward pass of gradient back-propagation with two contrastive forward passes, the FFA avoids several shortcomings undergone by its predecessor (e.g., vanishing/exploding gradient) by enabling layer-wise training heuristics. In classification tasks, this contrastive method has been proven to effectively create a latent sparse representation of the input data, ultimately favoring discriminability. However, FFA exhibits an inherent asymmetric gradient behavior due to an imbalanced loss function between positive and negative data, adversely impacting on the model's generalization capabilities and leading to an accuracy degradation. To address this issue, this work proposes the Symmetric Forward-Forward Algorithm (SFFA), a novel modification of the original FFA which partitions each layer into positive and negative neurons. This allows the local fitness function to be defined as the ratio between the activation of positive neurons and the overall layer activity, resulting in a symmetric loss landscape during the training phase. To evaluate the enhanced convergence of our method, we conduct several experiments using multiple image classification benchmarks, comparing the accuracy of models trained with SFFA to those trained with its FFA counterpart. As a byproduct of this reformulation, we explore the advantages of using a layer-wise training algorithm for Continual Learning (CL) tasks. The specialization of neurons and the sparsity of their activations induced by layer-wise training algorithms enable efficient CL strategies that incorporate new knowledge (classes) into the neural network, while preventing catastrophic forgetting of previously...

On the Improvement of Generalization and Stability of Forward-Only Learning via Neural Polarization

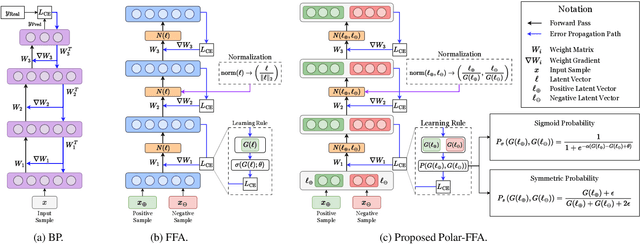
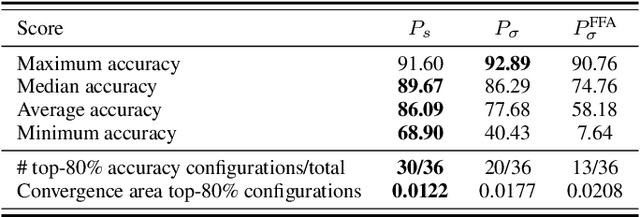
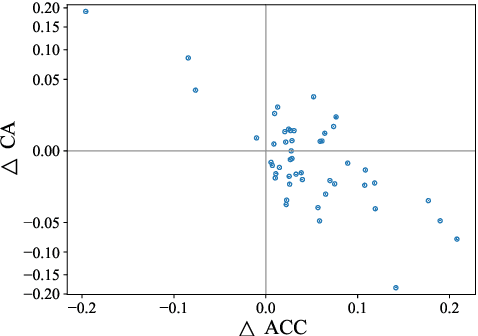
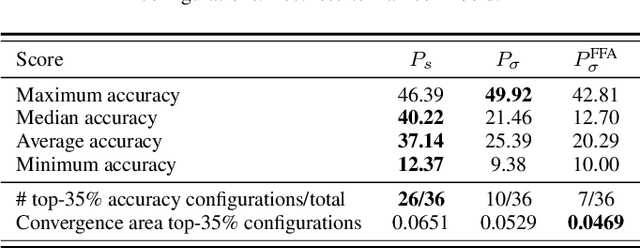
Forward-only learning algorithms have recently gained attention as alternatives to gradient backpropagation, replacing the backward step of this latter solver with an additional contrastive forward pass. Among these approaches, the so-called Forward-Forward Algorithm (FFA) has been shown to achieve competitive levels of performance in terms of generalization and complexity. Networks trained using FFA learn to contrastively maximize a layer-wise defined goodness score when presented with real data (denoted as positive samples) and to minimize it when processing synthetic data (corr. negative samples). However, this algorithm still faces weaknesses that negatively affect the model accuracy and training stability, primarily due to a gradient imbalance between positive and negative samples. To overcome this issue, in this work we propose a novel implementation of the FFA algorithm, denoted as Polar-FFA, which extends the original formulation by introducing a neural division (\emph{polarization}) between positive and negative instances. Neurons in each of these groups aim to maximize their goodness when presented with their respective data type, thereby creating a symmetric gradient behavior. To empirically gauge the improved learning capabilities of our proposed Polar-FFA, we perform several systematic experiments using different activation and goodness functions over image classification datasets. Our results demonstrate that Polar-FFA outperforms FFA in terms of accuracy and convergence speed. Furthermore, its lower reliance on hyperparameters reduces the need for hyperparameter tuning to guarantee optimal generalization capabilities, thereby allowing for a broader range of neural network configurations.

On the Robustness of Fully-Spiking Neural Networks in Open-World Scenarios using Forward-Only Learning Algorithms

In the last decade, Artificial Intelligence (AI) models have rapidly integrated into production pipelines propelled by their excellent modeling performance. However, the development of these models has not been matched by advancements in algorithms ensuring their safety, failing to guarantee robust behavior against Out-of-Distribution (OoD) inputs outside their learning domain. Furthermore, there is a growing concern with the sustainability of AI models and their required energy consumption in both training and inference phases. To mitigate these issues, this work explores the use of the Forward-Forward Algorithm (FFA), a biologically plausible alternative to Backpropagation, adapted to the spiking domain to enhance the overall energy efficiency of the model. By capitalizing on the highly expressive topology emerging from the latent space of models trained with FFA, we develop a novel FF-SCP algorithm for OoD Detection. Our approach measures the likelihood of a sample belonging to the in-distribution (ID) data by using the distance from the latent representation of samples to class-representative manifolds. Additionally, to provide deeper insights into our OoD pipeline, we propose a gradient-free attribution technique that highlights the features of a sample pushing it away from the distribution of any class. Multiple experiments using our spiking FFA adaptation demonstrate that the achieved accuracy levels are comparable to those seen in analog networks trained via back-propagation. Furthermore, OoD detection experiments on multiple datasets prove that FF-SCP outperforms avant-garde OoD detectors within the spiking domain in terms of several metrics used in this area. We also present a qualitative analysis of our explainability technique, exposing the precision by which the method detects OoD features, such as embedded artifacts or missing regions.

Emerging NeoHebbian Dynamics in Forward-Forward Learning: Implications for Neuromorphic Computing

Advances in neural computation have predominantly relied on the gradient backpropagation algorithm (BP). However, the recent shift towards non-stationary data modeling has highlighted the limitations of this heuristic, exposing that its adaptation capabilities are far from those seen in biological brains. Unlike BP, where weight updates are computed through a reverse error propagation path, Hebbian learning dynamics provide synaptic updates using only information within the layer itself. This has spurred interest in biologically plausible learning algorithms, hypothesized to overcome BP's shortcomings. In this context, Hinton recently introduced the Forward-Forward Algorithm (FFA), which employs local learning rules for each layer and has empirically proven its efficacy in multiple data modeling tasks. In this work we argue that when employing a squared Euclidean norm as a goodness function driving the local learning, the resulting FFA is equivalent to a neo-Hebbian Learning Rule. To verify this result, we compare the training behavior of FFA in analog networks with its Hebbian adaptation in spiking neural networks. Our experiments demonstrate that both versions of FFA produce similar accuracy and latent distributions. The findings herein reported provide empirical evidence linking biological learning rules with currently used training algorithms, thus paving the way towards extrapolating the positive outcomes from FFA to Hebbian learning rules. Simultaneously, our results imply that analog networks trained under FFA could be directly applied to neuromorphic computing, leading to reduced energy usage and increased computational speed.