On the Improvement of Generalization and Stability of Forward-Only Learning via Neural Polarization
Paper and Code
Aug 17, 2024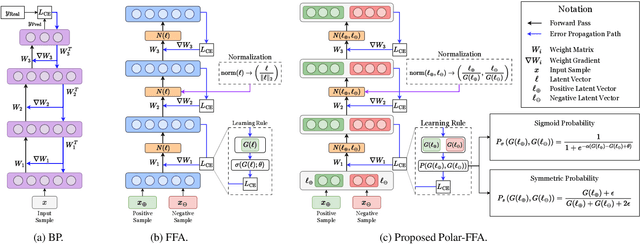
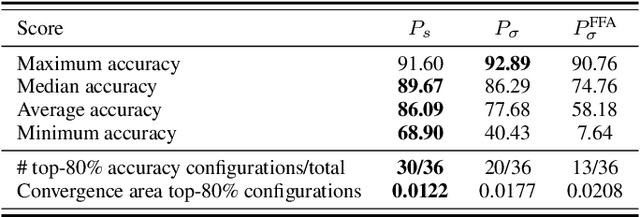
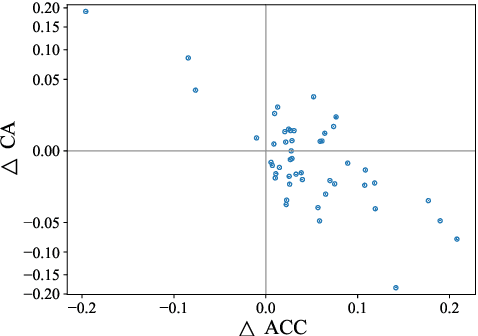
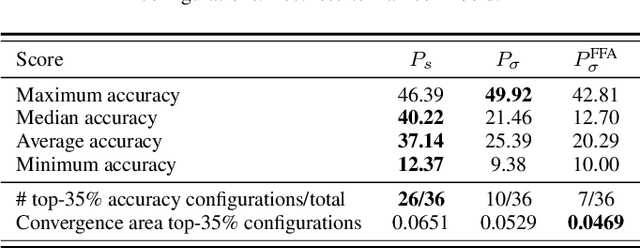
Forward-only learning algorithms have recently gained attention as alternatives to gradient backpropagation, replacing the backward step of this latter solver with an additional contrastive forward pass. Among these approaches, the so-called Forward-Forward Algorithm (FFA) has been shown to achieve competitive levels of performance in terms of generalization and complexity. Networks trained using FFA learn to contrastively maximize a layer-wise defined goodness score when presented with real data (denoted as positive samples) and to minimize it when processing synthetic data (corr. negative samples). However, this algorithm still faces weaknesses that negatively affect the model accuracy and training stability, primarily due to a gradient imbalance between positive and negative samples. To overcome this issue, in this work we propose a novel implementation of the FFA algorithm, denoted as Polar-FFA, which extends the original formulation by introducing a neural division (\emph{polarization}) between positive and negative instances. Neurons in each of these groups aim to maximize their goodness when presented with their respective data type, thereby creating a symmetric gradient behavior. To empirically gauge the improved learning capabilities of our proposed Polar-FFA, we perform several systematic experiments using different activation and goodness functions over image classification datasets. Our results demonstrate that Polar-FFA outperforms FFA in terms of accuracy and convergence speed. Furthermore, its lower reliance on hyperparameters reduces the need for hyperparameter tuning to guarantee optimal generalization capabilities, thereby allowing for a broader range of neural network configurations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge