A Tutorial on the Use of Physics-Informed Neural Networks to Compute the Spectrum of Quantum Systems

Quantum many-body systems are of great interest for many research areas, including physics, biology and chemistry. However, their simulation is extremely challenging, due to the exponential growth of the Hilbert space with the system size, making it exceedingly difficult to parameterize the wave functions of large systems by using exact methods. Neural networks and machine learning in general are a way to face this challenge. For instance, methods like Tensor networks and Neural Quantum States are being investigated as promising tools to obtain the wave function of a quantum mechanical system. In this tutorial, we focus on a particularly promising class of deep learning algorithms. We explain how to construct a Physics-Informed Neural Network (PINN) able to solve the Schr\"odinger equation for a given potential, by finding its eigenvalues and eigenfunctions. This technique is unsupervised, and utilizes a novel computational method in a manner that is barely explored. PINNs are a deep learning method that exploits Automatic Differentiation to solve Integro-Differential Equations in a mesh-free way. We show how to find both the ground and the excited states. The method discovers the states progressively by starting from the ground state. We explain how to introduce inductive biases in the loss to exploit further knowledge of the physical system. Such additional constraints allow for a faster and more accurate convergence. This technique can then be enhanced by a smart choice of collocation points in order to take advantage of the mesh-free nature of the PINN. The methods are made explicit by applying them to the infinite potential well and the particle in a ring, a challenging problem to be learned by an AI agent due to the presence of complex-valued eigenfunctions and degenerate states.

Quantum activation functions for quantum neural networks

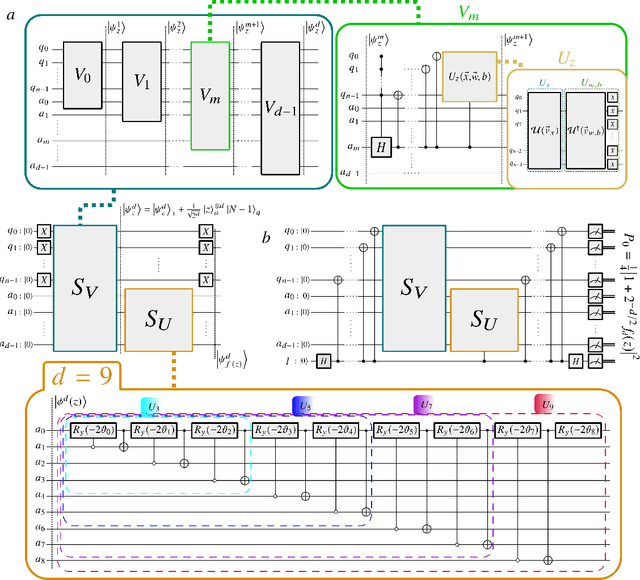
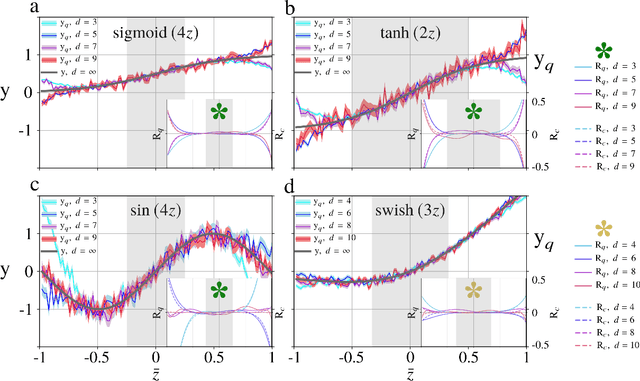
The field of artificial neural networks is expected to strongly benefit from recent developments of quantum computers. In particular, quantum machine learning, a class of quantum algorithms which exploit qubits for creating trainable neural networks, will provide more power to solve problems such as pattern recognition, clustering and machine learning in general. The building block of feed-forward neural networks consists of one layer of neurons connected to an output neuron that is activated according to an arbitrary activation function. The corresponding learning algorithm goes under the name of Rosenblatt perceptron. Quantum perceptrons with specific activation functions are known, but a general method to realize arbitrary activation functions on a quantum computer is still lacking. Here we fill this gap with a quantum algorithm which is capable to approximate any analytic activation functions to any given order of its power series. Unlike previous proposals providing irreversible measurement--based and simplified activation functions, here we show how to approximate any analytic function to any required accuracy without the need to measure the states encoding the information. Thanks to the generality of this construction, any feed-forward neural network may acquire the universal approximation properties according to Hornik's theorem. Our results recast the science of artificial neural networks in the architecture of gate-model quantum computers.

Quantum Semantic Learning by Reverse Annealing an Adiabatic Quantum Computer

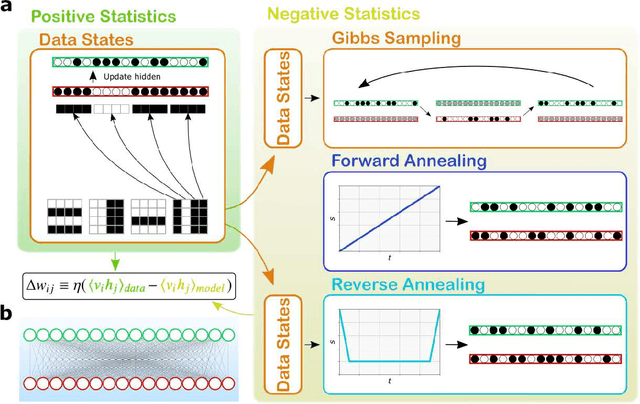
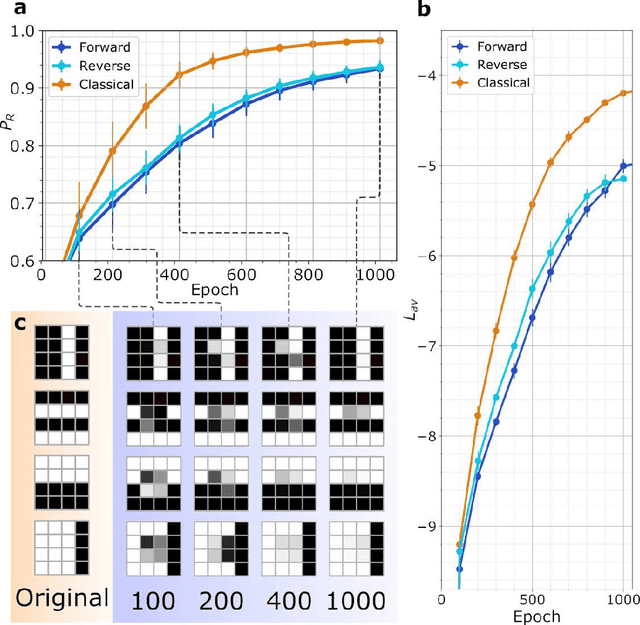
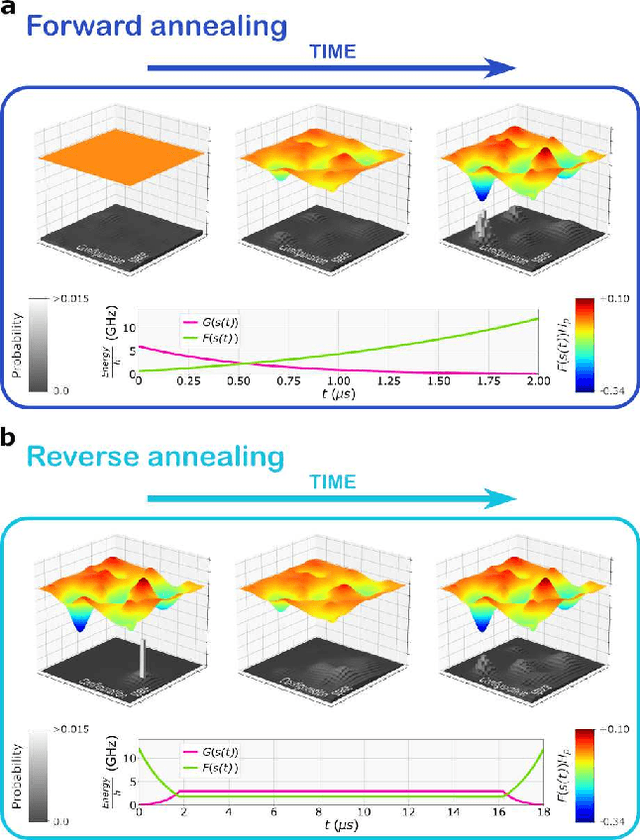
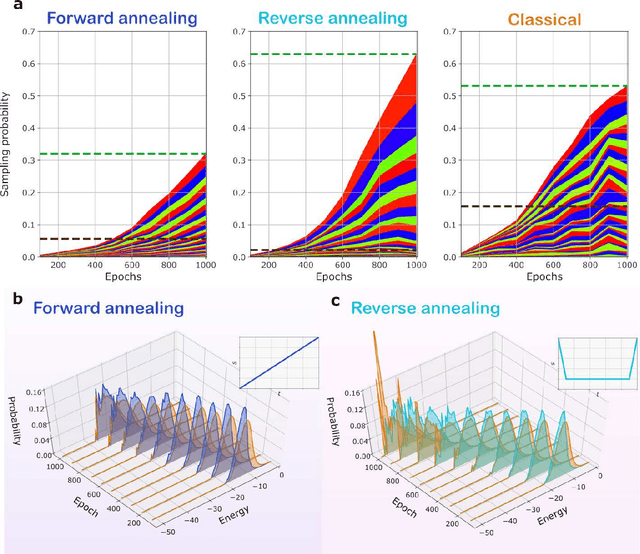
Boltzmann Machines constitute a class of neural networks with applications to image reconstruction, pattern classification and unsupervised learning in general. Their most common variants, called Restricted Boltzmann Machines (RBMs) exhibit a good trade-off between computability on existing silicon-based hardware and generality of possible applications. Still, the diffusion of RBMs is quite limited, since their training process proves to be hard. The advent of commercial Adiabatic Quantum Computers (AQCs) raised the expectation that the implementations of RBMs on such quantum devices could increase the training speed with respect to conventional hardware. To date, however, the implementation of RBM networks on AQCs has been limited by the low qubit connectivity when each qubit acts as a node of the neural network. Here we demonstrate the feasibility of a complete RBM on AQCs, thanks to an embedding that associates its nodes to virtual qubits, thus outperforming previous implementations based on incomplete graphs. Moreover, to accelerate the learning, we implement a semantic quantum search which, contrary to previous proposals, takes the input data as initial boundary conditions to start each learning step of the RBM, thanks to a reverse annealing schedule. Such an approach, unlike the more conventional forward annealing schedule, allows sampling configurations in a meaningful neighborhood of the training data, mimicking the behavior of the classical Gibbs sampling algorithm. We show that the learning based on reverse annealing quickly raises the sampling probability of a meaningful subset of the set of the configurations. Even without a proper optimization of the annealing schedule, the RBM semantically trained by reverse annealing achieves better scores on reconstruction tasks.

Control of the Correlation of Spontaneous Neuron Activity in Biological and Noise-activated CMOS Artificial Neural Microcircuits

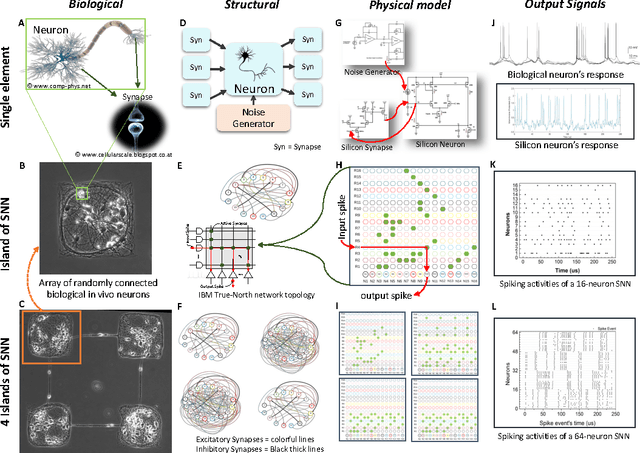
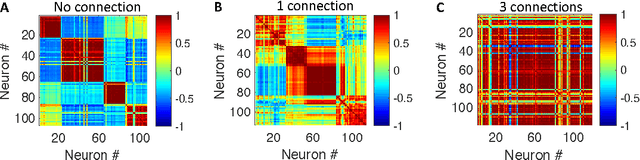
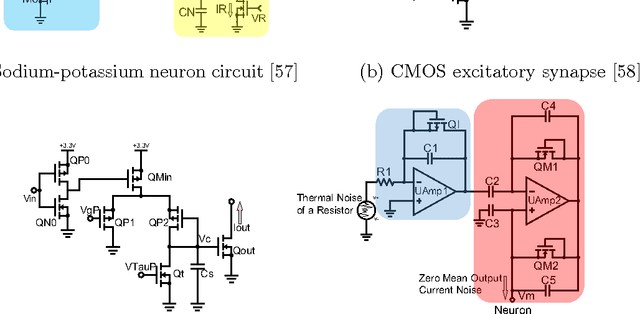
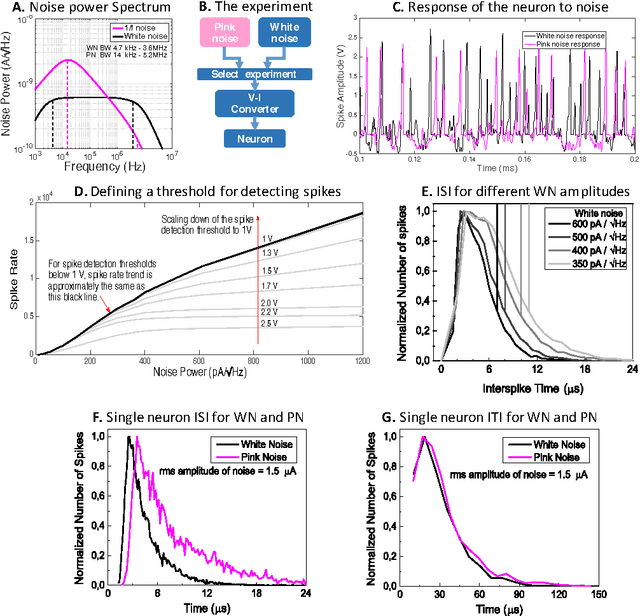
There are several indications that brain is organized not on a basis of individual unreliable neurons, but on a micro-circuital scale providing Lego blocks employed to create complex architectures. At such an intermediate scale, the firing activity in the microcircuits is governed by collective effects emerging by the background noise soliciting spontaneous firing, the degree of mutual connections between the neurons, and the topology of the connections. We compare spontaneous firing activity of small populations of neurons adhering to an engineered scaffold with simulations of biologically plausible CMOS artificial neuron populations whose spontaneous activity is ignited by tailored background noise. We provide a full set of flexible and low-power consuming silicon blocks including neurons, excitatory and inhibitory synapses, and both white and pink noise generators for spontaneous firing activation. We achieve a comparable degree of correlation of the firing activity of the biological neurons by controlling the kind and the number of connection among the silicon neurons. The correlation between groups of neurons, organized as a ring of four distinct populations connected by the equivalent of interneurons, is triggered more effectively by adding multiple synapses to the connections than increasing the number of independent point-to-point connections. The comparison between the biological and the artificial systems suggests that a considerable number of synapses is active also in biological populations adhering to engineered scaffolds.