Quantum activation functions for quantum neural networks

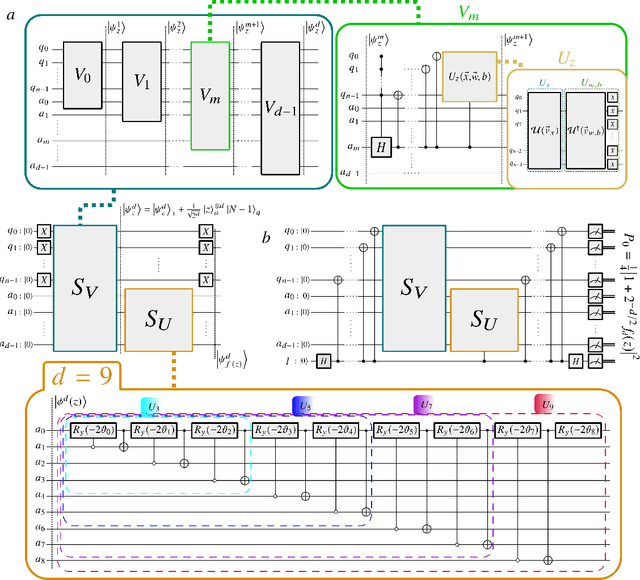
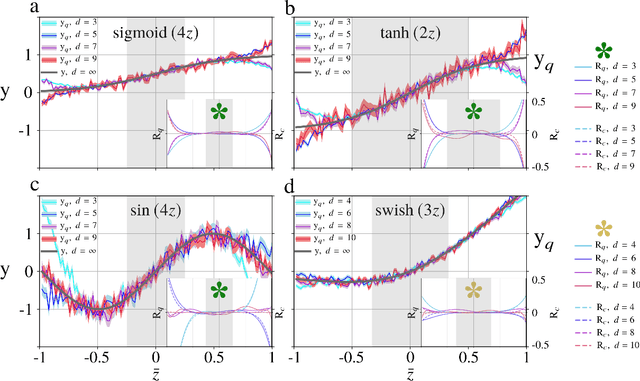
The field of artificial neural networks is expected to strongly benefit from recent developments of quantum computers. In particular, quantum machine learning, a class of quantum algorithms which exploit qubits for creating trainable neural networks, will provide more power to solve problems such as pattern recognition, clustering and machine learning in general. The building block of feed-forward neural networks consists of one layer of neurons connected to an output neuron that is activated according to an arbitrary activation function. The corresponding learning algorithm goes under the name of Rosenblatt perceptron. Quantum perceptrons with specific activation functions are known, but a general method to realize arbitrary activation functions on a quantum computer is still lacking. Here we fill this gap with a quantum algorithm which is capable to approximate any analytic activation functions to any given order of its power series. Unlike previous proposals providing irreversible measurement--based and simplified activation functions, here we show how to approximate any analytic function to any required accuracy without the need to measure the states encoding the information. Thanks to the generality of this construction, any feed-forward neural network may acquire the universal approximation properties according to Hornik's theorem. Our results recast the science of artificial neural networks in the architecture of gate-model quantum computers.

Quantum Semantic Learning by Reverse Annealing an Adiabatic Quantum Computer

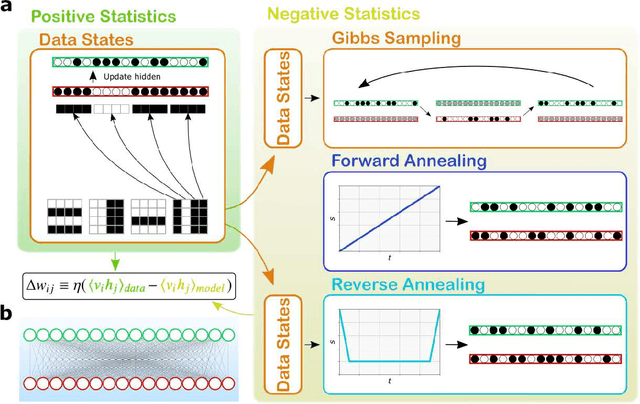
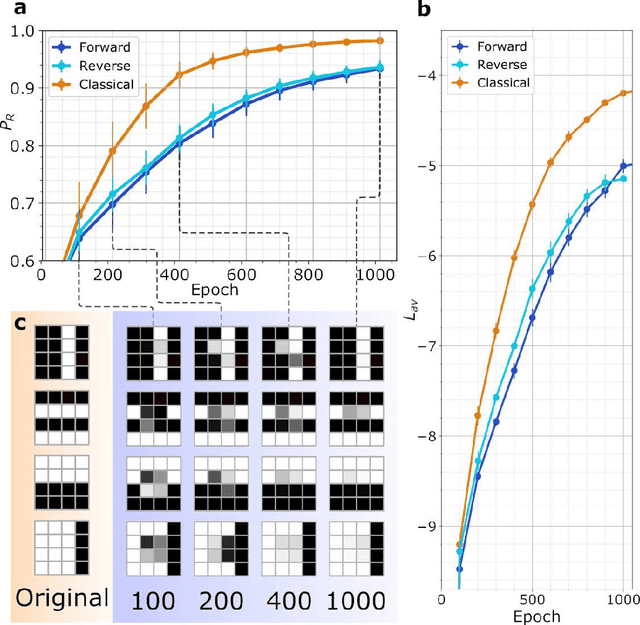
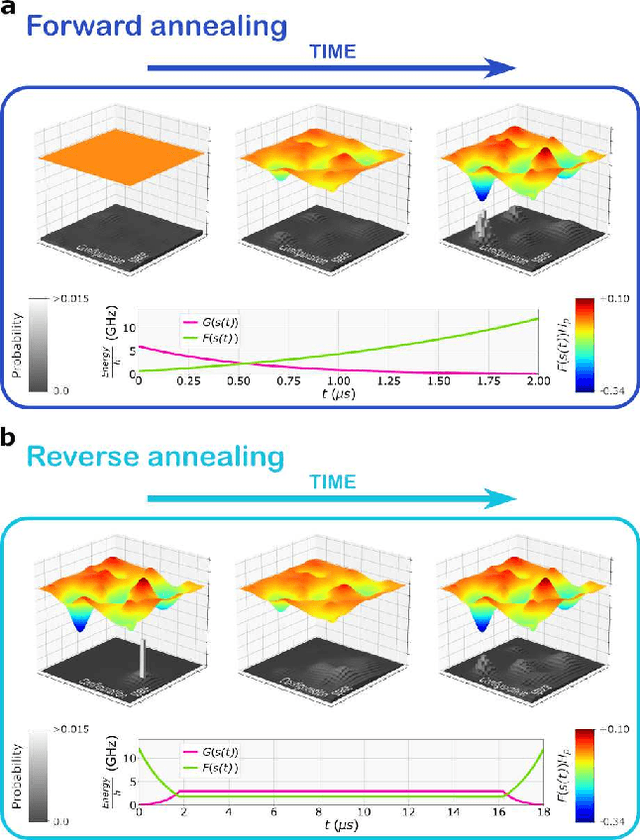
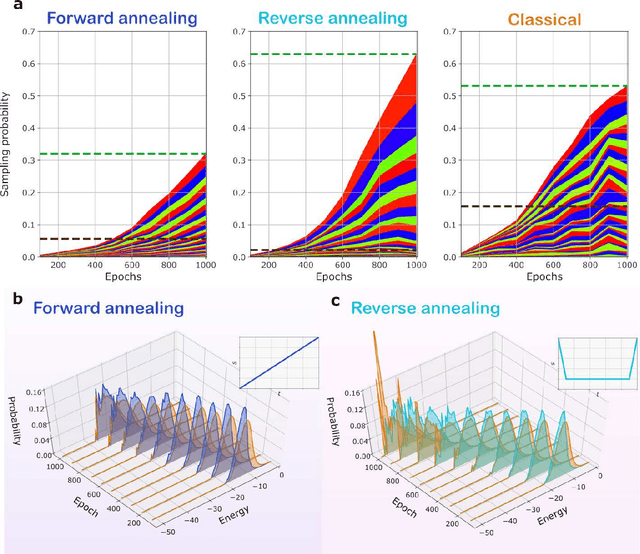
Boltzmann Machines constitute a class of neural networks with applications to image reconstruction, pattern classification and unsupervised learning in general. Their most common variants, called Restricted Boltzmann Machines (RBMs) exhibit a good trade-off between computability on existing silicon-based hardware and generality of possible applications. Still, the diffusion of RBMs is quite limited, since their training process proves to be hard. The advent of commercial Adiabatic Quantum Computers (AQCs) raised the expectation that the implementations of RBMs on such quantum devices could increase the training speed with respect to conventional hardware. To date, however, the implementation of RBM networks on AQCs has been limited by the low qubit connectivity when each qubit acts as a node of the neural network. Here we demonstrate the feasibility of a complete RBM on AQCs, thanks to an embedding that associates its nodes to virtual qubits, thus outperforming previous implementations based on incomplete graphs. Moreover, to accelerate the learning, we implement a semantic quantum search which, contrary to previous proposals, takes the input data as initial boundary conditions to start each learning step of the RBM, thanks to a reverse annealing schedule. Such an approach, unlike the more conventional forward annealing schedule, allows sampling configurations in a meaningful neighborhood of the training data, mimicking the behavior of the classical Gibbs sampling algorithm. We show that the learning based on reverse annealing quickly raises the sampling probability of a meaningful subset of the set of the configurations. Even without a proper optimization of the annealing schedule, the RBM semantically trained by reverse annealing achieves better scores on reconstruction tasks.