Optical identification using physical unclonable functions

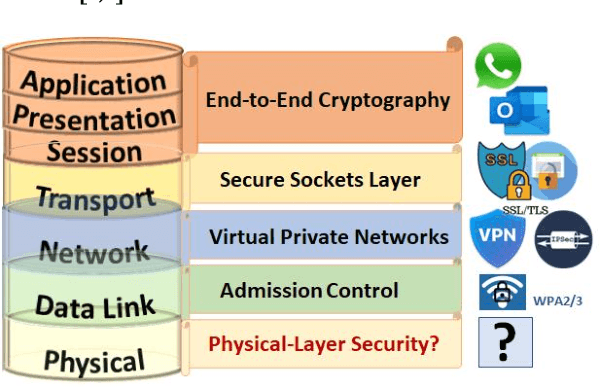
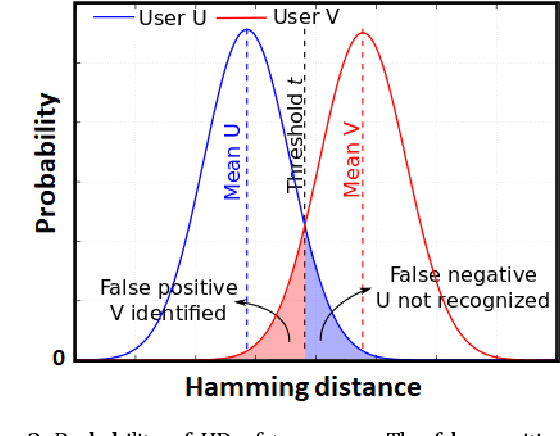
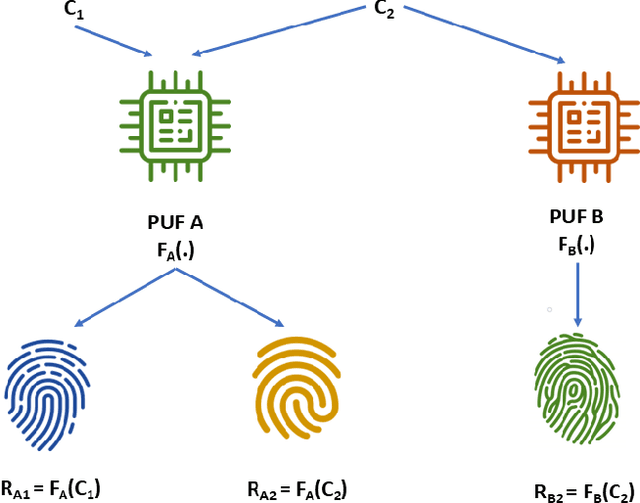
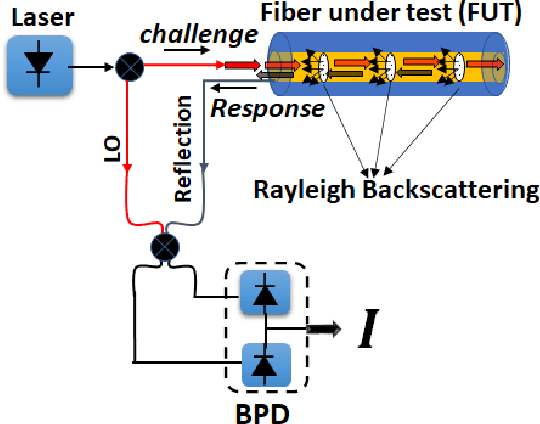
In this work, the concept of optical identification (OI) is introduced for the first time. The OI assigns an optical fingerprint and the corresponding digital signature to each sub-system of the network and estimates its reliability in different measures. We highlight the large potential applications of OI as a physical layer approach for security, identification, authentication, and monitoring purposes. To identify most of the sub-systems of a network, we propose to use the Rayleigh backscattering pattern, which is an optical physical unclonable function and allows to achieve OI with a simple procedure and without additional devices. The application of OI to fiber and path identification in a network, and to the authentication of the users in a quantum key distribution system are described.

On the Nonlinear Shaping Gain with Probabilistic Shaping and Carrier Phase Recovery

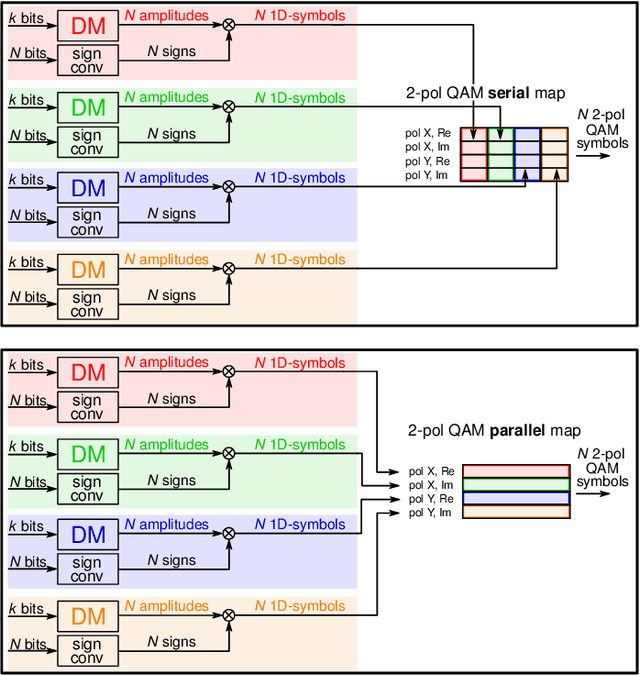
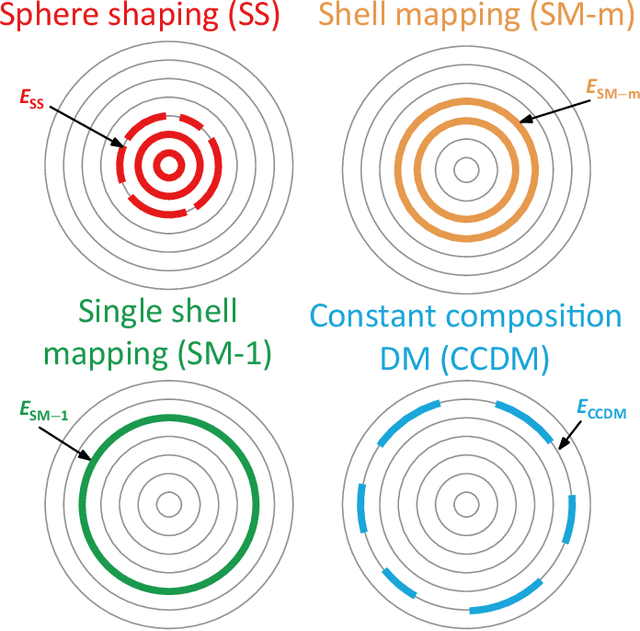
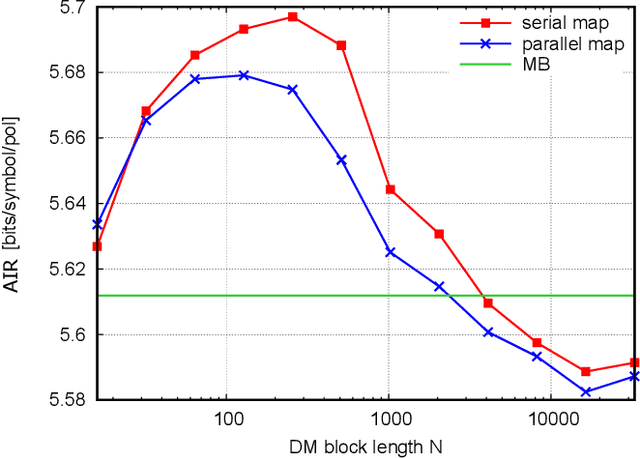
The performance of different probabilistic amplitude shaping (PAS) techniques in the nonlinear regime is investigated, highlighting its dependence on the PAS block length and the interaction with carrier phase recovery. Different PAS implementations are considered, based on different distribution matching (DM) techniques. When carrier phase recovery is not included, PAS with optimal block length provides a nonlinear shaping gain with respect to a linearly optimized PAS; among the considered DM techniques, the largest gain is obtained with sphere shaping. On the other hand, the nonlinear shaping gain becomes smaller, or completely vanishes, when carrier phase recovery is included, meaning that in this case all the considered implementations achieve a similar performance for a sufficiently long block length. Similar results are obtained in different link configurations, and also including laser phase noise, except when inline dispersion compensation is used. Furthermore, we define a new metric, the nonlinear phase noise (NPN) metric, which is based on the frequency resolved logarithmic perturbation model and explains the interaction of carrier phase recovery and PAS. We show that the NPN metric is highly correlated with the performance of the system. Our results suggest that, in general, the optimization of PAS in the nonlinear regime should always account for the presence of a carrier phase recovery algorithm. In this case, the reduction of the rate loss turns out to be more important than the mitigation of the nonlinear phase noise, the latter being already granted by the carrier phase recovery algorithm.