A New Twist on Low-Complexity Digital Backpropagation

This work proposes a novel low-complexity digital backpropagation (DBP) method, with the goal of optimizing the trade-off between backpropagation accuracy and complexity. The method combines a split step Fourier method (SSFM)-like structure with a simplifed logarithmic perturbation method to obtain a high accuracy with a small number of DBP steps. Subband processing and asymmetric steps with optimized splitting ratio are also employed to further reduce the number of steps. The first part of the manuscript is dedicated to the derivation of a simplified logaritmic-perturbation model for the propagation of a dual-polarization multiband signal in a fiber, which serves as a theoretical background for the development of the proposed coupled-band enhanced SSFM (CBESSFM). Next, the manuscript presents a digital signal processing algorithm for the implementation of DBP based on a discrete-time version of the model and an overlap-and-save processing strategy. A detailed analysis of the computational complexity of the algorithm is also presented. Finally, the performance and complexity of the proposed DBP method are investigated through numerical simulations. In a wavelength division multiplexing system over a 15 x 80km single mode fiber link, the proposed CB-ESSFM achieves a gain of about 1 dB over simple dispersion compensation with only 15 steps (corresponding to about 680 real multiplications per 2D symbol), with an improvement of 0.9 dB w.r.t. conventional SSFM and almost 0.4 dB w.r.t. our previously proposed ESSFM. Significant gains are obtained also at lower complexity. For instance, the gain reduces to a still significant value of 0.34 dB when a single DBP step is employed, requiring just 75 real multiplications per 2D symbol. A similar analysis is performed also for longer links, confirming the good performance of the proposed method w.r.t. the others.

Coupled-Band ESSFM for Low-Complexity DBP

We propose a novel digital backpropagation (DBP) technique that combines perturbation theory, subband processing, and splitting ratio optimization. We obtain 0.23 dB, 0.47 dB, or 0.91 dB gains w.r.t. dispersion compensation with only 74, 161, or 681 real multiplications/2D-symbol, improving significantly on existing DBP techniques.

Nonlinear Probabilistic Constellation Shaping with Sequence Selection

Probabilistic shaping is a pragmatic approach to improve the performance of coherent optical fiber communication systems. In the nonlinear regime, the advantages offered by probabilistic shaping might increase thanks to the opportunity to obtain an additional nonlinear shaping gain. Unfortunately, the optimization of conventional shaping techniques, such as probabilistic amplitude shaping (PAS), yields a relevant nonlinear shaping gain only in scenarios of limited practical interest. In this manuscript we use sequence selection to investigate the potential, opportunities, and challenges offered by nonlinear probabilistic shaping. First, we show that ideal sequence selection is able to provide up to 0.13 bit/s/Hz gain with respect to PAS with an optimized blocklength. However, this additional gain is obtained only if the selection metric accounts for the signs of the symbols: they must be known to compute the selection metric, but there is no need to shape them. Furthermore, we show that the selection depends in a non-critical way on the symbol rate and link length: the sequences selected for a certain scenario still provide a relevant gain if these are modified. Then, we analyze and compare several practical implementations of sequence selection by taking into account interaction with forward error correction (FEC) and complexity. Overall, the single block and the multi block FEC-independent bit scrambling are the best options, with a gain up to 0.08 bit/s/Hz. The main challenge and limitation to their practical implementation remains the evaluation of the metric, whose complexity is currently too high. Finally, we show that the nonlinear shaping gain provided by sequence selection persists when carrier phase recovery is included.

Practical Implementation of Sequence Selection for Nonlinear Probabilistic Shaping

We propose two novel techniques to implement sequence selection (SS) for fiber nonlinearity mitigation, demonstrating a nonlinear shaping gain of 0.24 bits/s/Hz, just 0.1 bits/s/Hz below the SS capacity lower bound.

On the Nonlinear Shaping Gain with Probabilistic Shaping and Carrier Phase Recovery

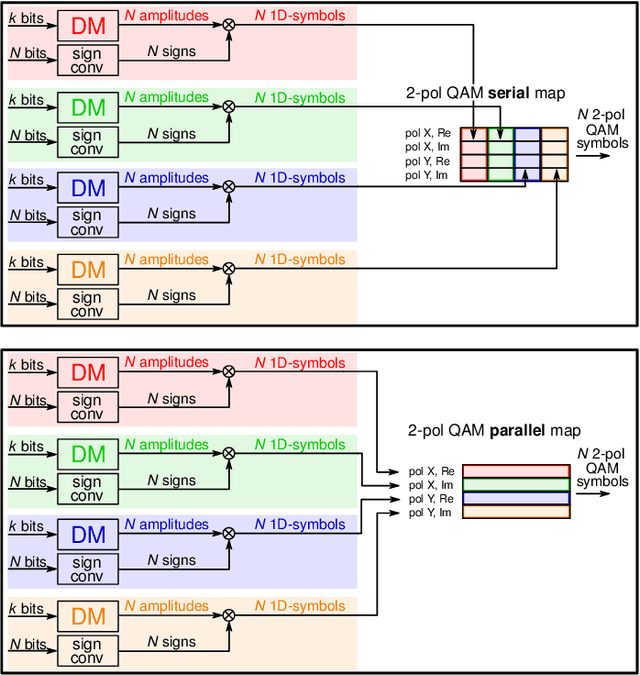
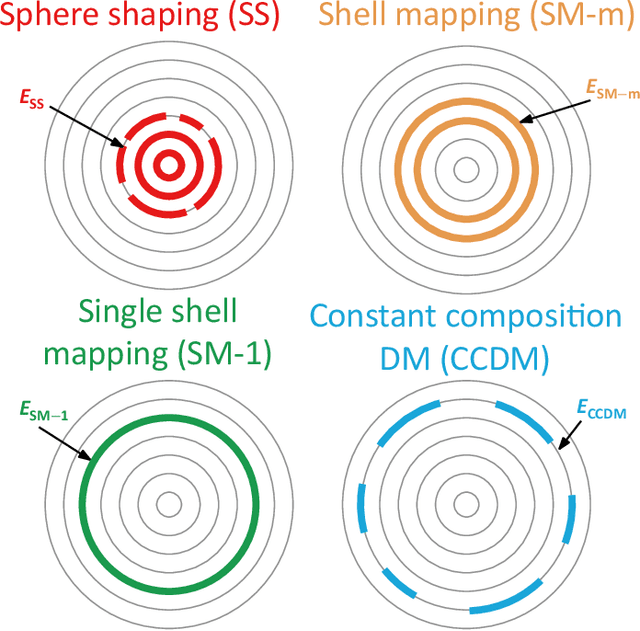
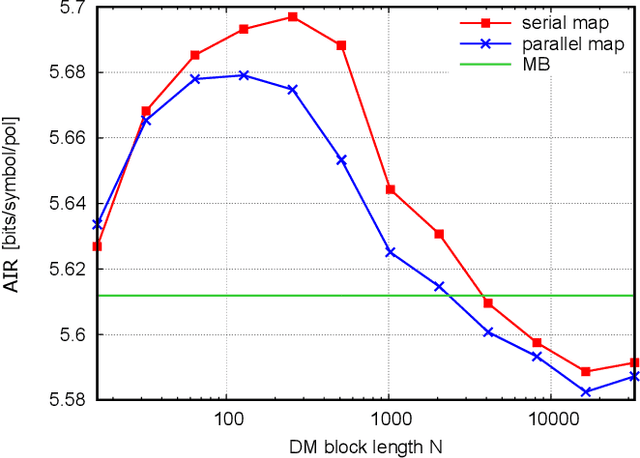
The performance of different probabilistic amplitude shaping (PAS) techniques in the nonlinear regime is investigated, highlighting its dependence on the PAS block length and the interaction with carrier phase recovery. Different PAS implementations are considered, based on different distribution matching (DM) techniques. When carrier phase recovery is not included, PAS with optimal block length provides a nonlinear shaping gain with respect to a linearly optimized PAS; among the considered DM techniques, the largest gain is obtained with sphere shaping. On the other hand, the nonlinear shaping gain becomes smaller, or completely vanishes, when carrier phase recovery is included, meaning that in this case all the considered implementations achieve a similar performance for a sufficiently long block length. Similar results are obtained in different link configurations, and also including laser phase noise, except when inline dispersion compensation is used. Furthermore, we define a new metric, the nonlinear phase noise (NPN) metric, which is based on the frequency resolved logarithmic perturbation model and explains the interaction of carrier phase recovery and PAS. We show that the NPN metric is highly correlated with the performance of the system. Our results suggest that, in general, the optimization of PAS in the nonlinear regime should always account for the presence of a carrier phase recovery algorithm. In this case, the reduction of the rate loss turns out to be more important than the mitigation of the nonlinear phase noise, the latter being already granted by the carrier phase recovery algorithm.

New Lower Bounds on the Capacity of Optical Fiber Channels via Optimized Shaping and Detection

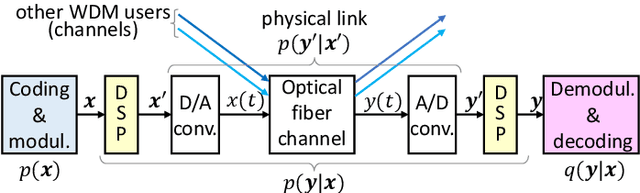
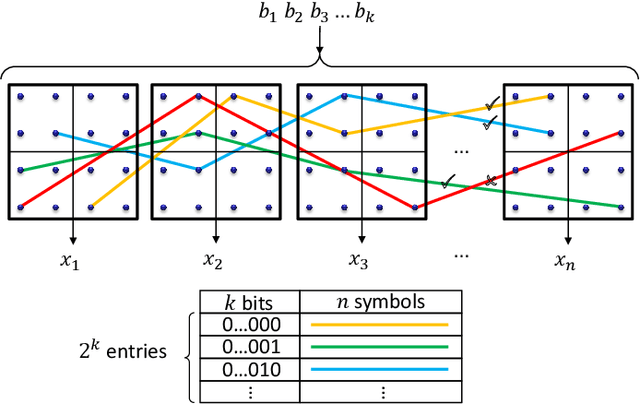
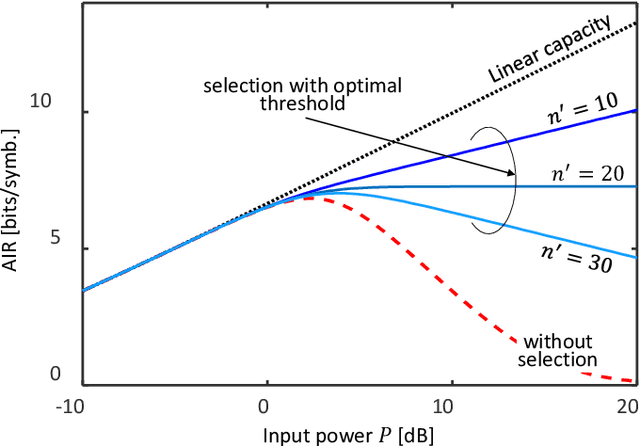
Constellation shaping is a practical and effective technique to improve the performance and the rate adaptivity of optical communication systems. In principle, it could also be used to mitigate the impact of nonlinear effects, possibly increasing the information rate beyond the current limit dictated by fiber nonlinearity. However, this appealing idea is frustrated by the difficulty of designing an effective shaping strategy that takes into account the nonlinearity and long memory of the fiber channel, as well as the possible interplay with other nonlinearity mitigation strategies. As a result, only little progress has been made so far, while the optimal shaping distribution and the ultimate channel capacity remain unknown. In this work, we describe a novel technique to optimize the shaping distribution in a very general setting and high-dimensional space. For a simplified block-memoryless nonlinear optical channel, the capacity lower bound obtained by the proposed technique can be expressed analytically, establishing the conditions for an unbounded growth of capacity with power. In a more realistic scenario, the technique can be implemented by a rejection sampling algorithm driven by a suitable cost function, and the corresponding achievable information rate estimated numerically. The combination of the proposed technique with an improved (non-Gaussian) decoding metric yields a new capacity lower bound for the dual-polarization WDM channel.

Tailored Shaping, Improved Detection, Simpler Backpropagation: the Road to Nonlinearity Mitigation

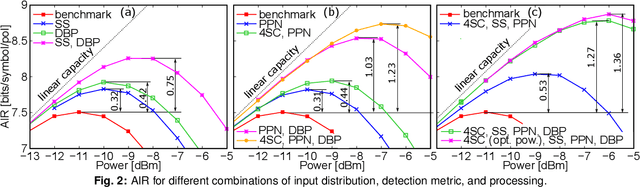
Several strategies for nonlinearity mitigation based on signal processing at the transmitter and/or receiver side are analyzed and their effectiveness is discussed. Improved capacity lower bounds based on their combination are presented.

A Sequence Selection Bound for the Capacity of the Nonlinear Fiber Channel

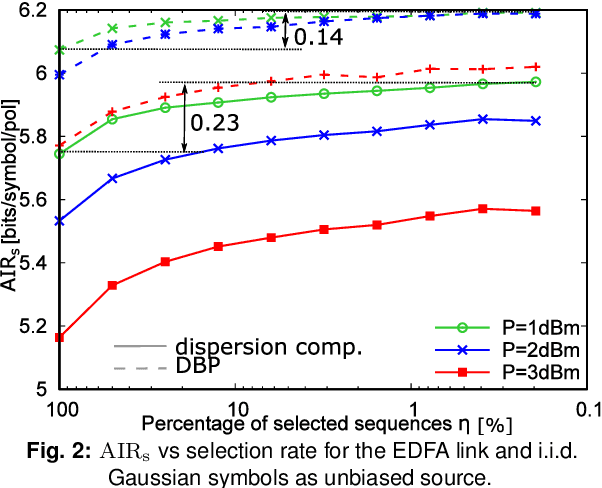
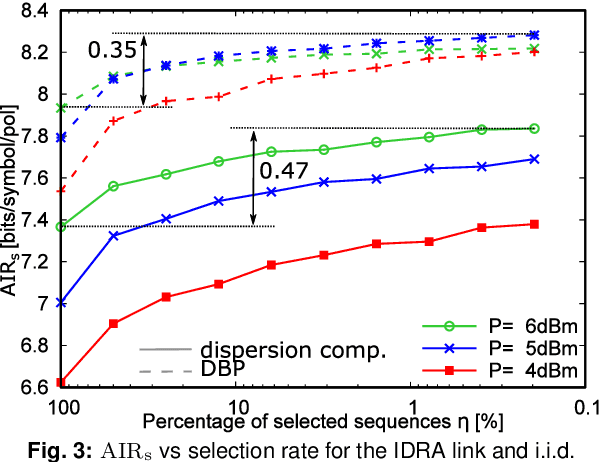
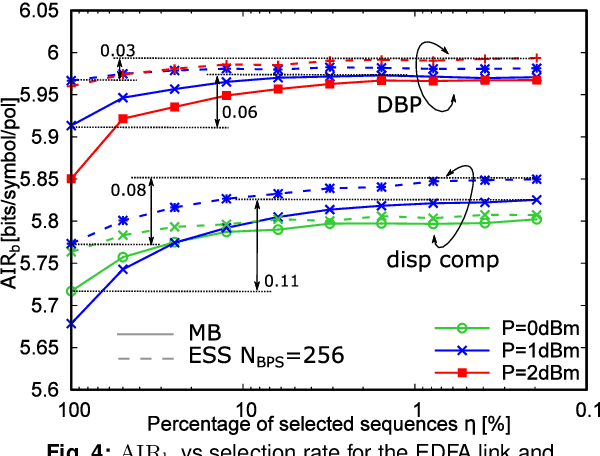
A novel technique to optimize the input distribution and compute a lower bound for the capacity of the nonlinear optical fiber channel is proposed. The technique improves previous bounds obtained with the additive white Gaussian noise decoding metric.