New Lower Bounds on the Capacity of Optical Fiber Channels via Optimized Shaping and Detection
Paper and Code
Dec 07, 2021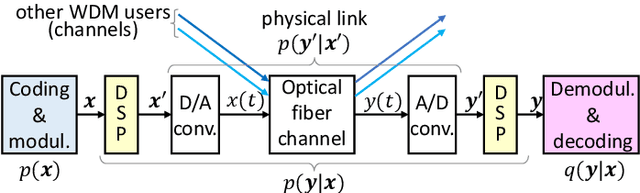
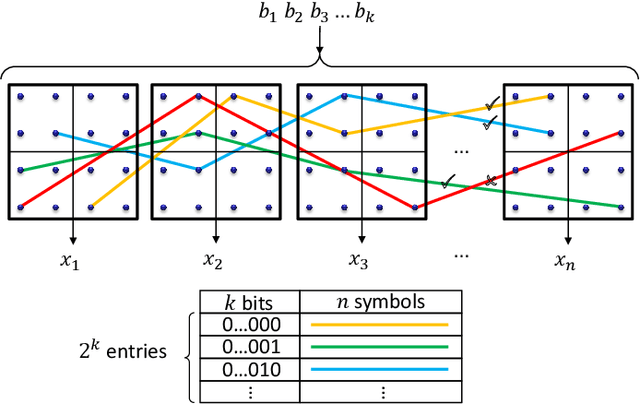

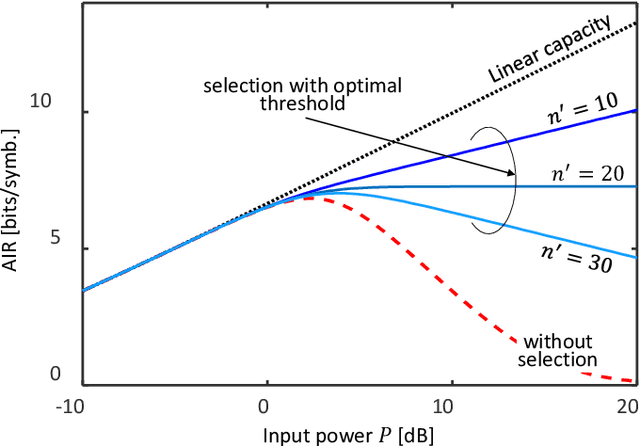
Constellation shaping is a practical and effective technique to improve the performance and the rate adaptivity of optical communication systems. In principle, it could also be used to mitigate the impact of nonlinear effects, possibly increasing the information rate beyond the current limit dictated by fiber nonlinearity. However, this appealing idea is frustrated by the difficulty of designing an effective shaping strategy that takes into account the nonlinearity and long memory of the fiber channel, as well as the possible interplay with other nonlinearity mitigation strategies. As a result, only little progress has been made so far, while the optimal shaping distribution and the ultimate channel capacity remain unknown. In this work, we describe a novel technique to optimize the shaping distribution in a very general setting and high-dimensional space. For a simplified block-memoryless nonlinear optical channel, the capacity lower bound obtained by the proposed technique can be expressed analytically, establishing the conditions for an unbounded growth of capacity with power. In a more realistic scenario, the technique can be implemented by a rejection sampling algorithm driven by a suitable cost function, and the corresponding achievable information rate estimated numerically. The combination of the proposed technique with an improved (non-Gaussian) decoding metric yields a new capacity lower bound for the dual-polarization WDM channel.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge