Emanuele Frandi
Fast and Scalable Lasso via Stochastic Frank-Wolfe Methods with a Convergence Guarantee
Oct 24, 2015



Abstract:Frank-Wolfe (FW) algorithms have been often proposed over the last few years as efficient solvers for a variety of optimization problems arising in the field of Machine Learning. The ability to work with cheap projection-free iterations and the incremental nature of the method make FW a very effective choice for many large-scale problems where computing a sparse model is desirable. In this paper, we present a high-performance implementation of the FW method tailored to solve large-scale Lasso regression problems, based on a randomized iteration, and prove that the convergence guarantees of the standard FW method are preserved in the stochastic setting. We show experimentally that our algorithm outperforms several existing state of the art methods, including the Coordinate Descent algorithm by Friedman et al. (one of the fastest known Lasso solvers), on several benchmark datasets with a very large number of features, without sacrificing the accuracy of the model. Our results illustrate that the algorithm is able to generate the complete regularization path on problems of size up to four million variables in less than one minute.
A PARTAN-Accelerated Frank-Wolfe Algorithm for Large-Scale SVM Classification
Feb 05, 2015



Abstract:Frank-Wolfe algorithms have recently regained the attention of the Machine Learning community. Their solid theoretical properties and sparsity guarantees make them a suitable choice for a wide range of problems in this field. In addition, several variants of the basic procedure exist that improve its theoretical properties and practical performance. In this paper, we investigate the application of some of these techniques to Machine Learning, focusing in particular on a Parallel Tangent (PARTAN) variant of the FW algorithm that has not been previously suggested or studied for this type of problems. We provide experiments both in a standard setting and using a stochastic speed-up technique, showing that the considered algorithms obtain promising results on several medium and large-scale benchmark datasets for SVM classification.
Complexity Issues and Randomization Strategies in Frank-Wolfe Algorithms for Machine Learning
Oct 15, 2014
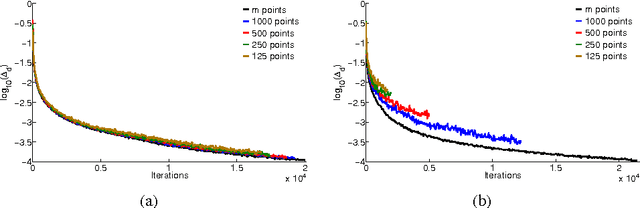


Abstract:Frank-Wolfe algorithms for convex minimization have recently gained considerable attention from the Optimization and Machine Learning communities, as their properties make them a suitable choice in a variety of applications. However, as each iteration requires to optimize a linear model, a clever implementation is crucial to make such algorithms viable on large-scale datasets. For this purpose, approximation strategies based on a random sampling have been proposed by several researchers. In this work, we perform an experimental study on the effectiveness of these techniques, analyze possible alternatives and provide some guidelines based on our results.
A Novel Frank-Wolfe Algorithm. Analysis and Applications to Large-Scale SVM Training
Oct 13, 2013



Abstract:Recently, there has been a renewed interest in the machine learning community for variants of a sparse greedy approximation procedure for concave optimization known as {the Frank-Wolfe (FW) method}. In particular, this procedure has been successfully applied to train large-scale instances of non-linear Support Vector Machines (SVMs). Specializing FW to SVM training has allowed to obtain efficient algorithms but also important theoretical results, including convergence analysis of training algorithms and new characterizations of model sparsity. In this paper, we present and analyze a novel variant of the FW method based on a new way to perform away steps, a classic strategy used to accelerate the convergence of the basic FW procedure. Our formulation and analysis is focused on a general concave maximization problem on the simplex. However, the specialization of our algorithm to quadratic forms is strongly related to some classic methods in computational geometry, namely the Gilbert and MDM algorithms. On the theoretical side, we demonstrate that the method matches the guarantees in terms of convergence rate and number of iterations obtained by using classic away steps. In particular, the method enjoys a linear rate of convergence, a result that has been recently proved for MDM on quadratic forms. On the practical side, we provide experiments on several classification datasets, and evaluate the results using statistical tests. Experiments show that our method is faster than the FW method with classic away steps, and works well even in the cases in which classic away steps slow down the algorithm. Furthermore, these improvements are obtained without sacrificing the predictive accuracy of the obtained SVM model.
* REVISED VERSION (October 2013) -- Title and abstract have been revised. Section 5 was added. Some proofs have been summarized (full-length proofs available in the previous version)
Training Support Vector Machines Using Frank-Wolfe Optimization Methods
Dec 04, 2012



Abstract:Training a Support Vector Machine (SVM) requires the solution of a quadratic programming problem (QP) whose computational complexity becomes prohibitively expensive for large scale datasets. Traditional optimization methods cannot be directly applied in these cases, mainly due to memory restrictions. By adopting a slightly different objective function and under mild conditions on the kernel used within the model, efficient algorithms to train SVMs have been devised under the name of Core Vector Machines (CVMs). This framework exploits the equivalence of the resulting learning problem with the task of building a Minimal Enclosing Ball (MEB) problem in a feature space, where data is implicitly embedded by a kernel function. In this paper, we improve on the CVM approach by proposing two novel methods to build SVMs based on the Frank-Wolfe algorithm, recently revisited as a fast method to approximate the solution of a MEB problem. In contrast to CVMs, our algorithms do not require to compute the solutions of a sequence of increasingly complex QPs and are defined by using only analytic optimization steps. Experiments on a large collection of datasets show that our methods scale better than CVMs in most cases, sometimes at the price of a slightly lower accuracy. As CVMs, the proposed methods can be easily extended to machine learning problems other than binary classification. However, effective classifiers are also obtained using kernels which do not satisfy the condition required by CVMs and can thus be used for a wider set of problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge