The Adaptive $τ$-Lasso: Its Robustness and Oracle Properties

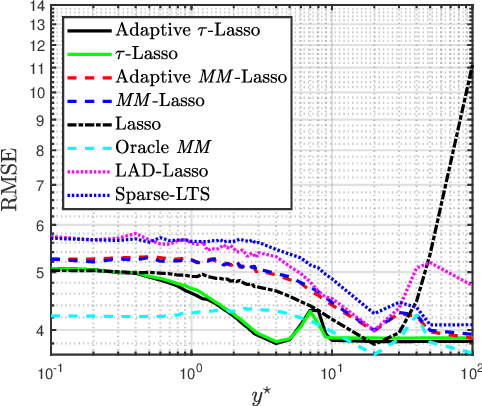
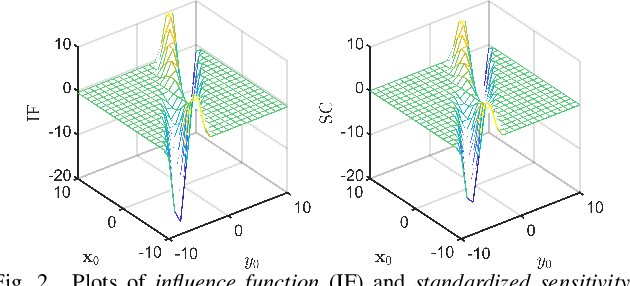
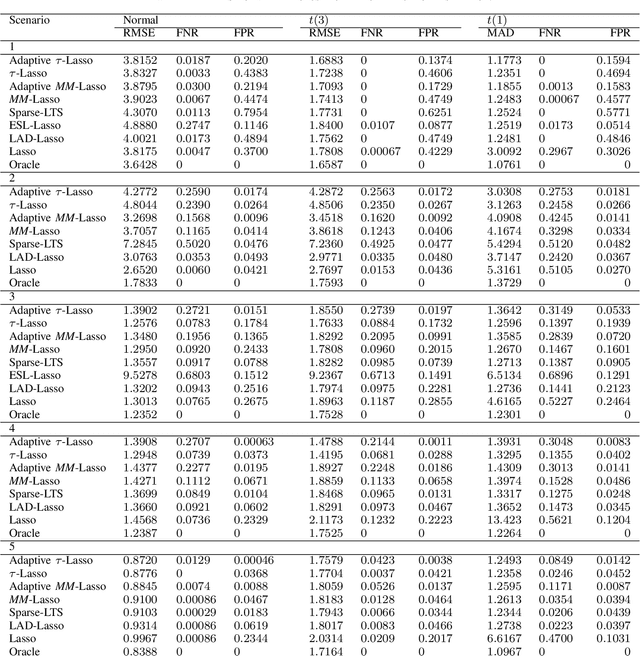
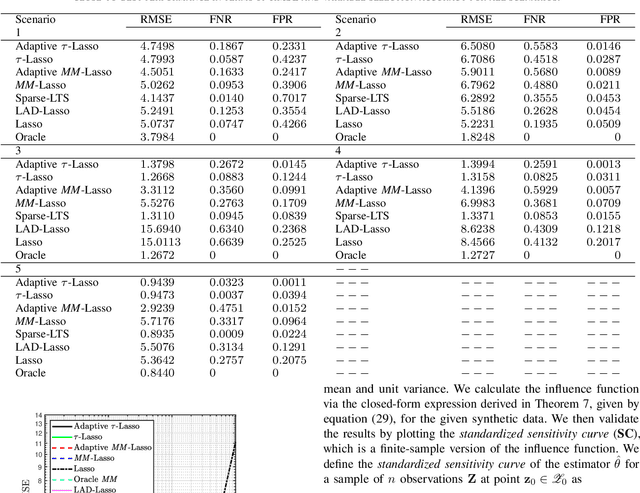
This paper introduces a new regularized version of the robust $\tau$-regression estimator for analyzing high-dimensional data sets subject to gross contamination in the response variables and covariates. We call the resulting estimator adaptive $\tau$-Lasso that is robust to outliers and high-leverage points and simultaneously employs adaptive $\ell_1$-norm penalty term to reduce the bias associated with large true regression coefficients. More specifically, this adaptive $\ell_1$-norm penalty term assigns a weight to each regression coefficient. For a fixed number of predictors $p$, we show that the adaptive $\tau$-Lasso has the oracle property with respect to variable-selection consistency and asymptotic normality for the regression vector corresponding to the true support, assuming knowledge of the true regression vector support. We then characterize its robustness via the finite-sample breakdown point and the influence function. We carry-out extensive simulations to compare the performance of the adaptive $\tau$-Lasso estimator with that of other competing regularized estimators in terms of prediction and variable selection accuracy in the presence of contamination within the response vector/regression matrix and additive heavy-tailed noise. We observe from our simulations that the class of $\tau$-Lasso estimators exhibits robustness and reliable performance in both contaminated and uncontaminated data settings, achieving the best or close-to-best for many scenarios, except for oracle estimators. However, it is worth noting that no particular estimator uniformly dominates others. We also validate our findings on robustness properties through simulation experiments.

Two-Stage Robust and Sparse Distributed Statistical Inference for Large-Scale Data

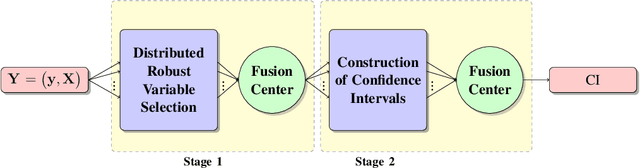
In this paper, we address the problem of conducting statistical inference in settings involving large-scale data that may be high-dimensional and contaminated by outliers. The high volume and dimensionality of the data require distributed processing and storage solutions. We propose a two-stage distributed and robust statistical inference procedures coping with high-dimensional models by promoting sparsity. In the first stage, known as model selection, relevant predictors are locally selected by applying robust Lasso estimators to the distinct subsets of data. The variable selections from each computation node are then fused by a voting scheme to find the sparse basis for the complete data set. It identifies the relevant variables in a robust manner. In the second stage, the developed statistically robust and computationally efficient bootstrap methods are employed. The actual inference constructs confidence intervals, finds parameter estimates and quantifies standard deviation. Similar to stage 1, the results of local inference are communicated to the fusion center and combined there. By using analytical methods, we establish the favorable statistical properties of the robust and computationally efficient bootstrap methods including consistency for a fixed number of predictors, and robustness. The proposed two-stage robust and distributed inference procedures demonstrate reliable performance and robustness in variable selection, finding confidence intervals and bootstrap approximations of standard deviations even when data is high-dimensional and contaminated by outliers.