The Adaptive $τ$-Lasso: Its Robustness and Oracle Properties

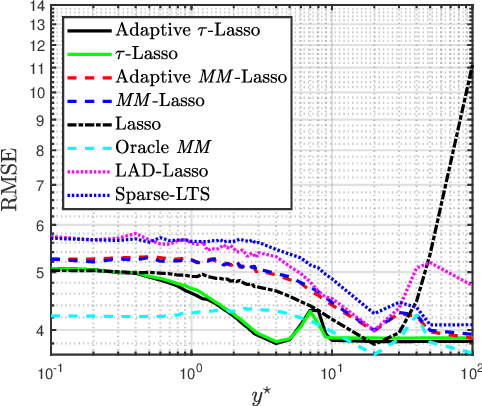
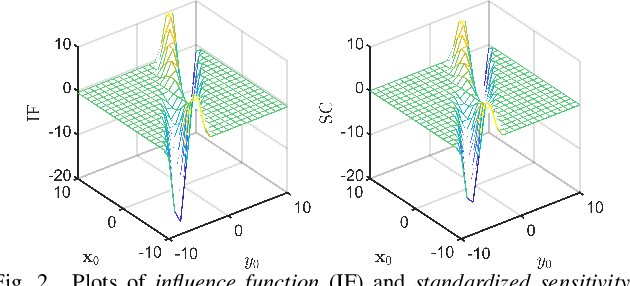
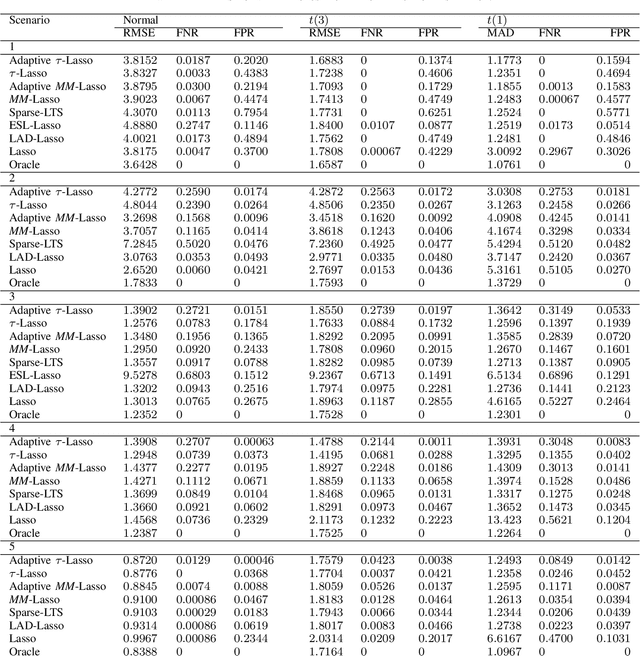
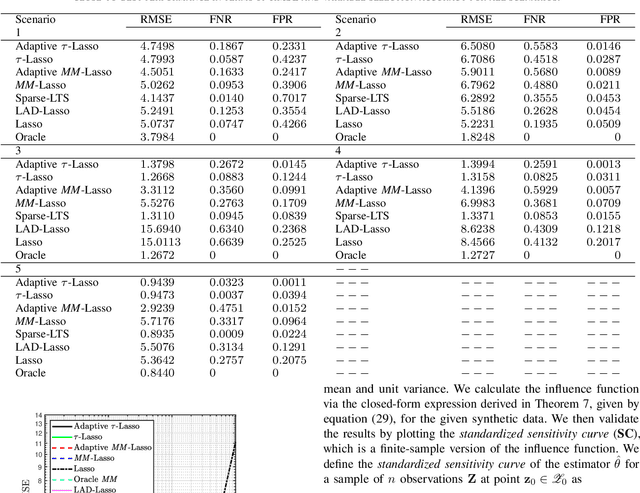
This paper introduces a new regularized version of the robust $\tau$-regression estimator for analyzing high-dimensional data sets subject to gross contamination in the response variables and covariates. We call the resulting estimator adaptive $\tau$-Lasso that is robust to outliers and high-leverage points and simultaneously employs adaptive $\ell_1$-norm penalty term to reduce the bias associated with large true regression coefficients. More specifically, this adaptive $\ell_1$-norm penalty term assigns a weight to each regression coefficient. For a fixed number of predictors $p$, we show that the adaptive $\tau$-Lasso has the oracle property with respect to variable-selection consistency and asymptotic normality for the regression vector corresponding to the true support, assuming knowledge of the true regression vector support. We then characterize its robustness via the finite-sample breakdown point and the influence function. We carry-out extensive simulations to compare the performance of the adaptive $\tau$-Lasso estimator with that of other competing regularized estimators in terms of prediction and variable selection accuracy in the presence of contamination within the response vector/regression matrix and additive heavy-tailed noise. We observe from our simulations that the class of $\tau$-Lasso estimators exhibits robustness and reliable performance in both contaminated and uncontaminated data settings, achieving the best or close-to-best for many scenarios, except for oracle estimators. However, it is worth noting that no particular estimator uniformly dominates others. We also validate our findings on robustness properties through simulation experiments.