DeepDFA: Automata Learning through Neural Probabilistic Relaxations

In this work, we introduce DeepDFA, a novel approach to identifying Deterministic Finite Automata (DFAs) from traces, harnessing a differentiable yet discrete model. Inspired by both the probabilistic relaxation of DFAs and Recurrent Neural Networks (RNNs), our model offers interpretability post-training, alongside reduced complexity and enhanced training efficiency compared to traditional RNNs. Moreover, by leveraging gradient-based optimization, our method surpasses combinatorial approaches in both scalability and noise resilience. Validation experiments conducted on target regular languages of varying size and complexity demonstrate that our approach is accurate, fast, and robust to noise in both the input symbols and the output labels of training data, integrating the strengths of both logical grammar induction and deep learning.

Neural Reward Machines

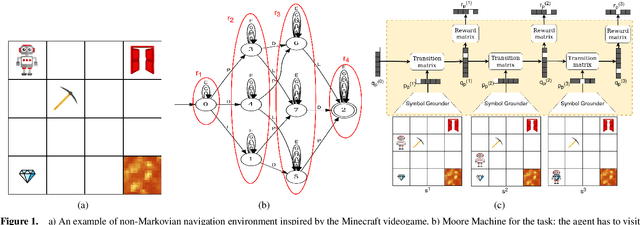
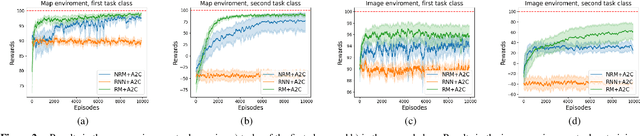
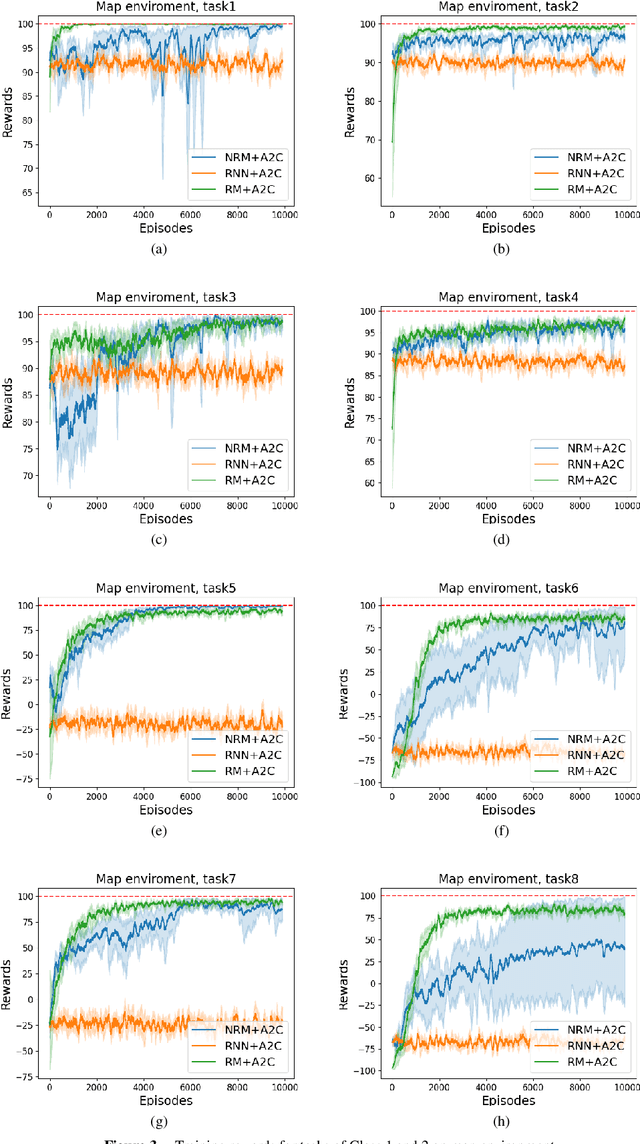
Non-markovian Reinforcement Learning (RL) tasks are very hard to solve, because agents must consider the entire history of state-action pairs to act rationally in the environment. Most works use symbolic formalisms (as Linear Temporal Logic or automata) to specify the temporally-extended task. These approaches only work in finite and discrete state environments or continuous problems for which a mapping between the raw state and a symbolic interpretation is known as a symbol grounding (SG) function. Here, we define Neural Reward Machines (NRM), an automata-based neurosymbolic framework that can be used for both reasoning and learning in non-symbolic non-markovian RL domains, which is based on the probabilistic relaxation of Moore Machines. We combine RL with semisupervised symbol grounding (SSSG) and we show that NRMs can exploit high-level symbolic knowledge in non-symbolic environments without any knowledge of the SG function, outperforming Deep RL methods which cannot incorporate prior knowledge. Moreover, we advance the research in SSSG, proposing an algorithm for analysing the groundability of temporal specifications, which is more efficient than baseline techniques of a factor $10^3$.