On Linear Convergence in Smooth Convex-Concave Bilinearly-Coupled Saddle-Point Optimization: Lower Bounds and Optimal Algorithms

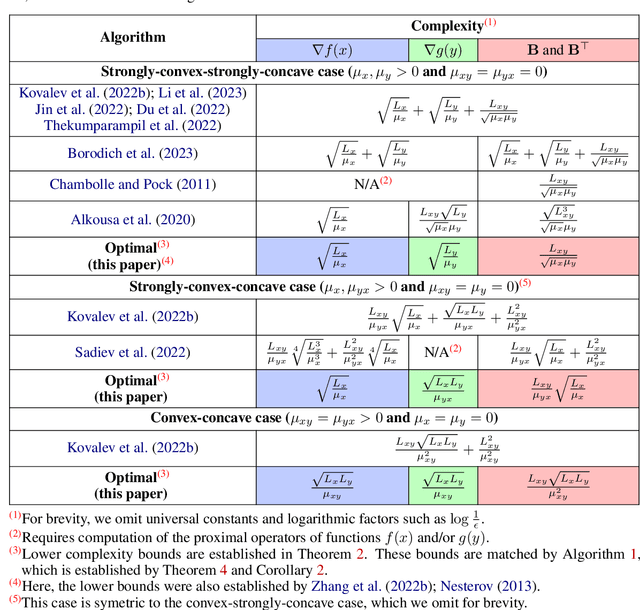
We revisit the smooth convex-concave bilinearly-coupled saddle-point problem of the form $\min_x\max_y f(x) + \langle y,\mathbf{B} x\rangle - g(y)$. In the highly specific case where each of the functions $f(x)$ and $g(y)$ is either affine or strongly convex, there exist lower bounds on the number of gradient evaluations and matrix-vector multiplications required to solve the problem, as well as matching optimal algorithms. A notable aspect of these algorithms is that they are able to attain linear convergence, i.e., the number of iterations required to solve the problem is proportional to $\log(1/\epsilon)$. However, the class of bilinearly-coupled saddle-point problems for which linear convergence is possible is much wider and can involve smooth non-strongly convex functions $f(x)$ and $g(y)$. Therefore, we develop the first lower complexity bounds and matching optimal linearly converging algorithms for this problem class. Our lower complexity bounds are much more general, but they cover and unify the existing results in the literature. On the other hand, our algorithm implements the separation of complexities, which, for the first time, enables the simultaneous achievement of both optimal gradient evaluation and matrix-vector multiplication complexities, resulting in the best theoretical performance to date.

Optimal Gradient Sliding and its Application to Distributed Optimization Under Similarity

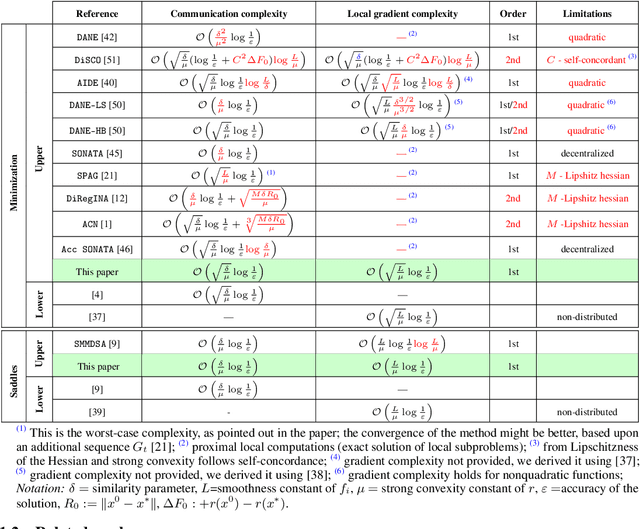
We study structured convex optimization problems, with additive objective $r:=p + q$, where $r$ is ($\mu$-strongly) convex, $q$ is $L_q$-smooth and convex, and $p$ is $L_p$-smooth, possibly nonconvex. For such a class of problems, we proposed an inexact accelerated gradient sliding method that can skip the gradient computation for one of these components while still achieving optimal complexity of gradient calls of $p$ and $q$, that is, $\mathcal{O}(\sqrt{L_p/\mu})$ and $\mathcal{O}(\sqrt{L_q/\mu})$, respectively. This result is much sharper than the classic black-box complexity $\mathcal{O}(\sqrt{(L_p+L_q)/\mu})$, especially when the difference between $L_q$ and $L_q$ is large. We then apply the proposed method to solve distributed optimization problems over master-worker architectures, under agents' function similarity, due to statistical data similarity or otherwise. The distributed algorithm achieves for the first time lower complexity bounds on {\it both} communication and local gradient calls, with the former having being a long-standing open problem. Finally the method is extended to distributed saddle-problems (under function similarity) by means of solving a class of variational inequalities, achieving lower communication and computation complexity bounds.