Edward Pearce-Crump
Permutation Equivariant Neural Networks for Symmetric Tensors
Mar 14, 2025
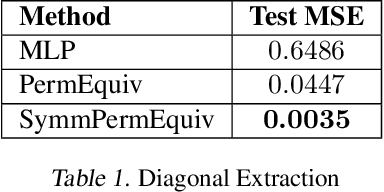

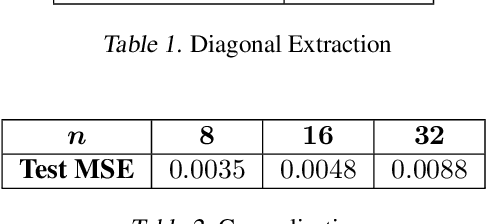
Abstract:Incorporating permutation equivariance into neural networks has proven to be useful in ensuring that models respect symmetries that exist in data. Symmetric tensors, which naturally appear in statistics, machine learning, and graph theory, are essential for many applications in physics, chemistry, and materials science, amongst others. However, existing research on permutation equivariant models has not explored symmetric tensors as inputs, and most prior work on learning from these tensors has focused on equivariance to Euclidean groups. In this paper, we present two different characterisations of all linear permutation equivariant functions between symmetric power spaces of $\mathbb{R}^n$. We show on two tasks that these functions are highly data efficient compared to standard MLPs and have potential to generalise well to symmetric tensors of different sizes.
A Diagrammatic Approach to Improve Computational Efficiency in Group Equivariant Neural Networks
Dec 14, 2024Abstract:Group equivariant neural networks are growing in importance owing to their ability to generalise well in applications where the data has known underlying symmetries. Recent characterisations of a class of these networks that use high-order tensor power spaces as their layers suggest that they have significant potential; however, their implementation remains challenging owing to the prohibitively expensive nature of the computations that are involved. In this work, we present a fast matrix multiplication algorithm for any equivariant weight matrix that maps between tensor power layer spaces in these networks for four groups: the symmetric, orthogonal, special orthogonal, and symplectic groups. We obtain this algorithm by developing a diagrammatic framework based on category theory that enables us to not only express each weight matrix as a linear combination of diagrams but also makes it possible for us to use these diagrams to factor the original computation into a series of steps that are optimal. We show that this algorithm improves the Big-$O$ time complexity exponentially in comparison to a na\"{i}ve matrix multiplication.
Compact Matrix Quantum Group Equivariant Neural Networks
Nov 10, 2023Abstract:We derive the existence of a new type of neural network, called a compact matrix quantum group equivariant neural network, that learns from data that has an underlying quantum symmetry. We apply the Woronowicz formulation of Tannaka-Krein duality to characterise the weight matrices that appear in these neural networks for any easy compact matrix quantum group. We show that compact matrix quantum group equivariant neural networks contain, as a subclass, all compact matrix group equivariant neural networks. Moreover, we obtain characterisations of the weight matrices for many compact matrix group equivariant neural networks that have not previously appeared in the machine learning literature.
Graph Automorphism Group Equivariant Neural Networks
Jul 15, 2023



Abstract:For any graph $G$ having $n$ vertices and its automorphism group $\textrm{Aut}(G)$, we provide a full characterisation of all of the possible $\textrm{Aut}(G)$-equivariant neural networks whose layers are some tensor power of $\mathbb{R}^{n}$. In particular, we find a spanning set of matrices for the learnable, linear, $\textrm{Aut}(G)$-equivariant layer functions between such tensor power spaces in the standard basis of $\mathbb{R}^{n}$.
Categorification of Group Equivariant Neural Networks
Apr 27, 2023

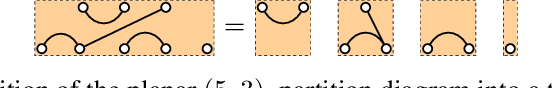

Abstract:We present a novel application of category theory for deep learning. We show how category theory can be used to understand and work with the linear layer functions of group equivariant neural networks whose layers are some tensor power space of $\mathbb{R}^{n}$ for the groups $S_n$, $O(n)$, $Sp(n)$, and $SO(n)$. By using category theoretic constructions, we build a richer structure that is not seen in the original formulation of these neural networks, leading to new insights. In particular, we outline the development of an algorithm for quickly computing the result of a vector that is passed through an equivariant, linear layer for each group in question. The success of our approach suggests that category theory could be beneficial for other areas of deep learning.
An Algorithm for Computing with Brauer's Group Equivariant Neural Network Layers
Apr 27, 2023
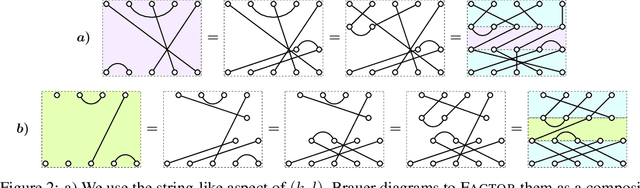
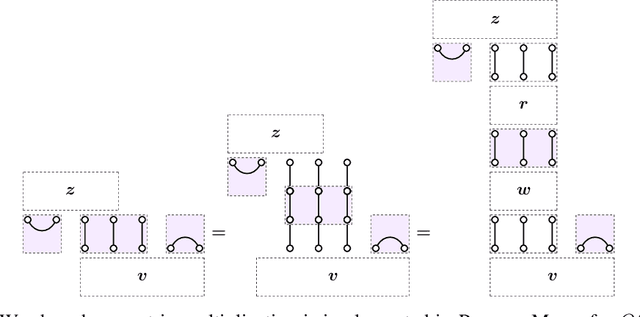
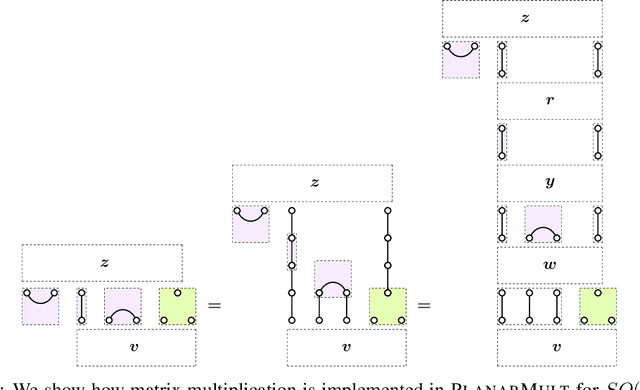
Abstract:The learnable, linear neural network layers between tensor power spaces of $\mathbb{R}^{n}$ that are equivariant to the orthogonal group, $O(n)$, the special orthogonal group, $SO(n)$, and the symplectic group, $Sp(n)$, were characterised in arXiv:2212.08630. We present an algorithm for multiplying a vector by any weight matrix for each of these groups, using category theoretic constructions to implement the procedure. We achieve a significant reduction in computational cost compared with a naive implementation by making use of Kronecker product matrices to perform the multiplication. We show that our approach extends to the symmetric group, $S_n$, recovering the algorithm of arXiv:2303.06208 in the process.
How Jellyfish Characterise Alternating Group Equivariant Neural Networks
Jan 24, 2023Abstract:We provide a full characterisation of all of the possible alternating group ($A_n$) equivariant neural networks whose layers are some tensor power of $\mathbb{R}^{n}$. In particular, we find a basis of matrices for the learnable, linear, $A_n$-equivariant layer functions between such tensor power spaces in the standard basis of $\mathbb{R}^{n}$. We also describe how our approach generalises to the construction of neural networks that are equivariant to local symmetries.
Connecting Permutation Equivariant Neural Networks and Partition Diagrams
Dec 16, 2022

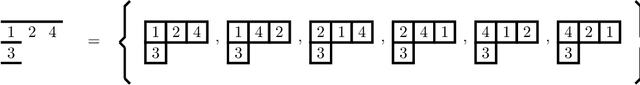
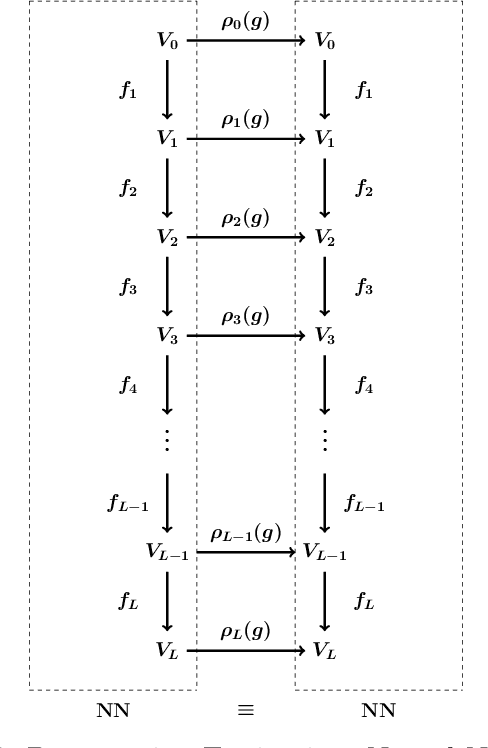
Abstract:We show how the Schur-Weyl duality that exists between the partition algebra and the symmetric group results in a stronger theoretical foundation for characterising all of the possible permutation equivariant neural networks whose layers are some tensor power of the permutation representation $M_n$ of the symmetric group $S_n$. In doing so, we unify two separate bodies of literature, and we correct some of the major results that are now widely quoted by the machine learning community. In particular, we find a basis of matrices for the learnable, linear, permutation equivariant layer functions between such tensor power spaces in the standard basis of $M_n$ by using an elegant graphical representation of a basis of set partitions for the partition algebra and its related vector spaces. Also, we show how we can calculate the number of weights that must appear in these layer functions by looking at certain paths through the McKay quiver for $M_n$. Finally, we describe how our approach generalises to the construction of neural networks that are equivariant to local symmetries.
Brauer's Group Equivariant Neural Networks
Dec 16, 2022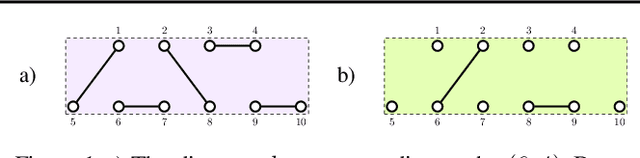
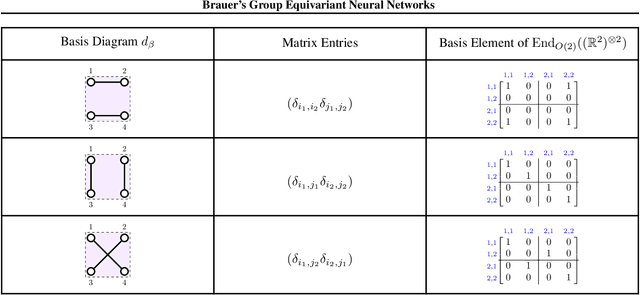
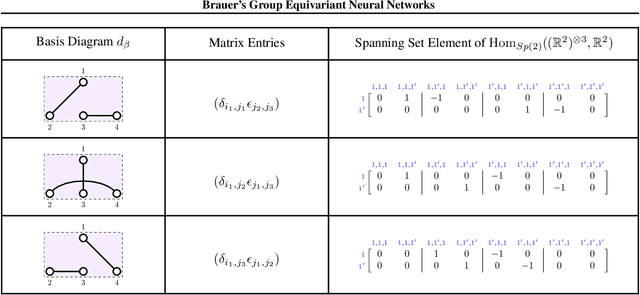
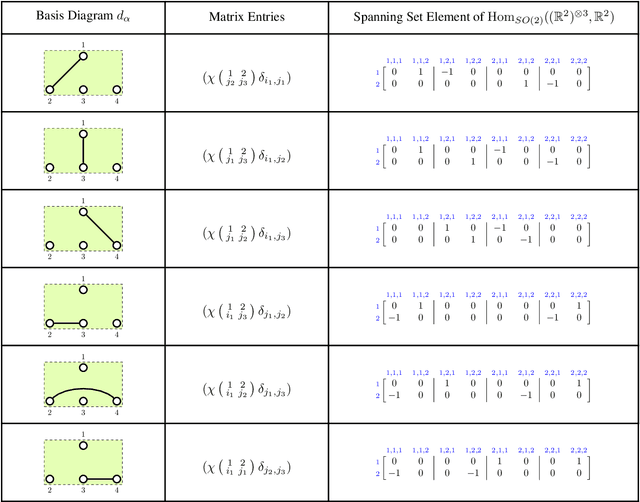
Abstract:We provide a full characterisation of all of the possible group equivariant neural networks whose layers are some tensor power of $\mathbb{R}^{n}$ for three symmetry groups that are missing from the machine learning literature: $O(n)$, the orthogonal group; $SO(n)$, the special orthogonal group; and $Sp(n)$, the symplectic group. In particular, we find a spanning set of matrices for the learnable, linear, equivariant layer functions between such tensor power spaces in the standard basis of $\mathbb{R}^{n}$ when the group is $O(n)$ or $SO(n)$, and in the symplectic basis of $\mathbb{R}^{n}$ when the group is $Sp(n)$. The neural networks that we characterise are simple to implement since our method circumvents the typical requirement when building group equivariant neural networks of having to decompose the tensor power spaces of $\mathbb{R}^{n}$ into irreducible representations. We also describe how our approach generalises to the construction of neural networks that are equivariant to local symmetries. The theoretical background for our results comes from the Schur-Weyl dualities that were established by Brauer in his 1937 paper "On Algebras Which are Connected with the Semisimple Continuous Groups" for each of the three groups in question. We suggest that Schur-Weyl duality is a powerful mathematical concept that could be used to understand the structure of neural networks that are equivariant to groups beyond those considered in this paper.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge