Permutation Equivariant Neural Networks for Symmetric Tensors
Paper and Code
Mar 14, 2025
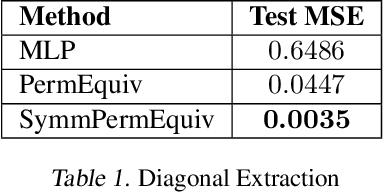

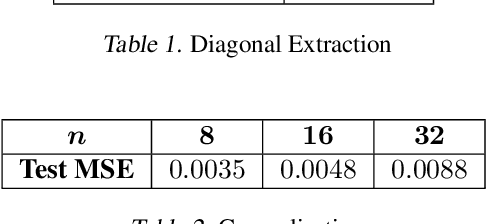
Incorporating permutation equivariance into neural networks has proven to be useful in ensuring that models respect symmetries that exist in data. Symmetric tensors, which naturally appear in statistics, machine learning, and graph theory, are essential for many applications in physics, chemistry, and materials science, amongst others. However, existing research on permutation equivariant models has not explored symmetric tensors as inputs, and most prior work on learning from these tensors has focused on equivariance to Euclidean groups. In this paper, we present two different characterisations of all linear permutation equivariant functions between symmetric power spaces of $\mathbb{R}^n$. We show on two tasks that these functions are highly data efficient compared to standard MLPs and have potential to generalise well to symmetric tensors of different sizes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge