Brauer's Group Equivariant Neural Networks

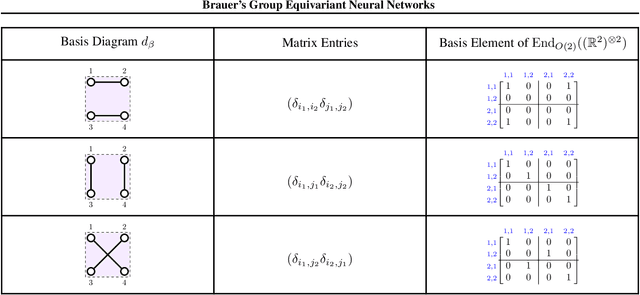
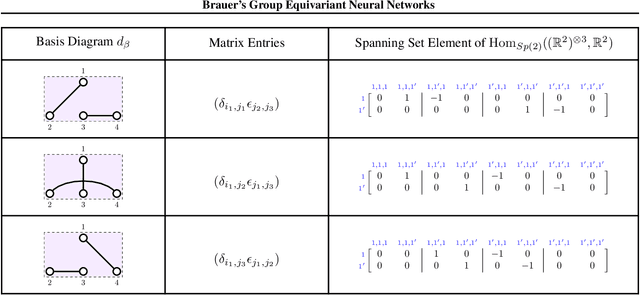
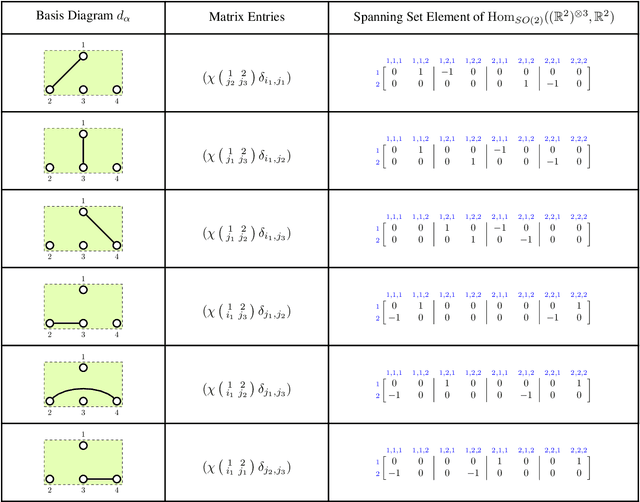
We provide a full characterisation of all of the possible group equivariant neural networks whose layers are some tensor power of $\mathbb{R}^{n}$ for three symmetry groups that are missing from the machine learning literature: $O(n)$, the orthogonal group; $SO(n)$, the special orthogonal group; and $Sp(n)$, the symplectic group. In particular, we find a spanning set of matrices for the learnable, linear, equivariant layer functions between such tensor power spaces in the standard basis of $\mathbb{R}^{n}$ when the group is $O(n)$ or $SO(n)$, and in the symplectic basis of $\mathbb{R}^{n}$ when the group is $Sp(n)$. The neural networks that we characterise are simple to implement since our method circumvents the typical requirement when building group equivariant neural networks of having to decompose the tensor power spaces of $\mathbb{R}^{n}$ into irreducible representations. We also describe how our approach generalises to the construction of neural networks that are equivariant to local symmetries. The theoretical background for our results comes from the Schur-Weyl dualities that were established by Brauer in his 1937 paper "On Algebras Which are Connected with the Semisimple Continuous Groups" for each of the three groups in question. We suggest that Schur-Weyl duality is a powerful mathematical concept that could be used to understand the structure of neural networks that are equivariant to groups beyond those considered in this paper.