A Diagrammatic Approach to Improve Computational Efficiency in Group Equivariant Neural Networks

Group equivariant neural networks are growing in importance owing to their ability to generalise well in applications where the data has known underlying symmetries. Recent characterisations of a class of these networks that use high-order tensor power spaces as their layers suggest that they have significant potential; however, their implementation remains challenging owing to the prohibitively expensive nature of the computations that are involved. In this work, we present a fast matrix multiplication algorithm for any equivariant weight matrix that maps between tensor power layer spaces in these networks for four groups: the symmetric, orthogonal, special orthogonal, and symplectic groups. We obtain this algorithm by developing a diagrammatic framework based on category theory that enables us to not only express each weight matrix as a linear combination of diagrams but also makes it possible for us to use these diagrams to factor the original computation into a series of steps that are optimal. We show that this algorithm improves the Big-$O$ time complexity exponentially in comparison to a na\"{i}ve matrix multiplication.

Time-series Transformer Generative Adversarial Networks

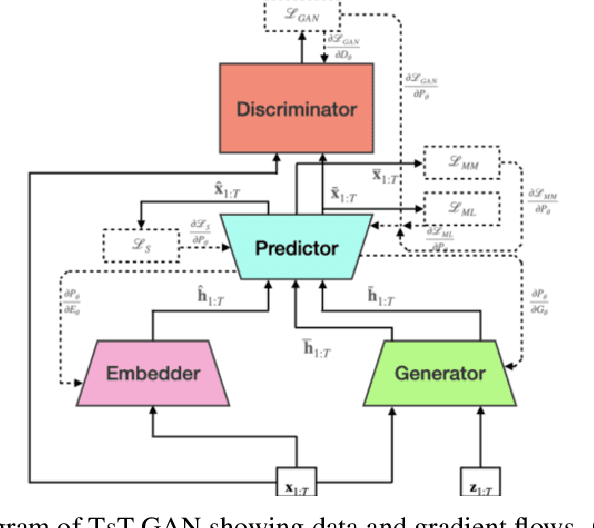
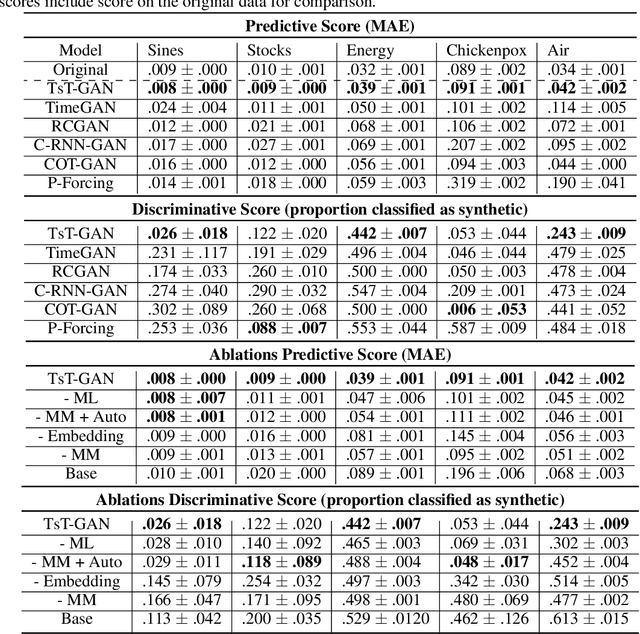
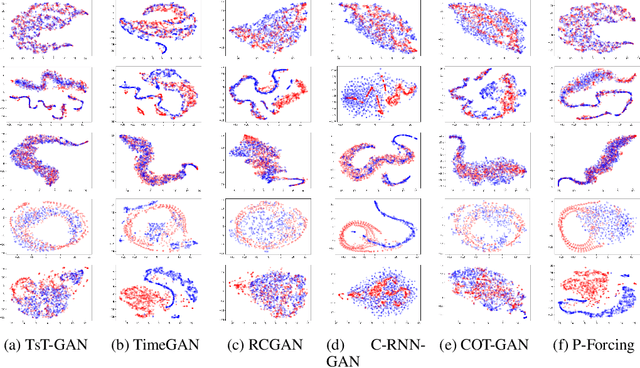
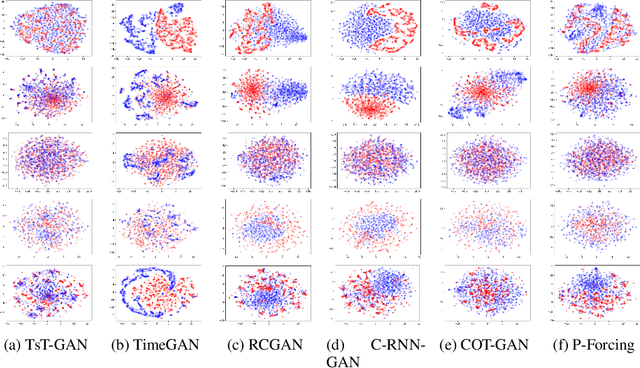
Many real-world tasks are plagued by limitations on data: in some instances very little data is available and in others, data is protected by privacy enforcing regulations (e.g. GDPR). We consider limitations posed specifically on time-series data and present a model that can generate synthetic time-series which can be used in place of real data. A model that generates synthetic time-series data has two objectives: 1) to capture the stepwise conditional distribution of real sequences, and 2) to faithfully model the joint distribution of entire real sequences. Autoregressive models trained via maximum likelihood estimation can be used in a system where previous predictions are fed back in and used to predict future ones; in such models, errors can accrue over time. Furthermore, a plausible initial value is required making MLE based models not really generative. Many downstream tasks learn to model conditional distributions of the time-series, hence, synthetic data drawn from a generative model must satisfy 1) in addition to performing 2). We present TsT-GAN, a framework that capitalises on the Transformer architecture to satisfy the desiderata and compare its performance against five state-of-the-art models on five datasets and show that TsT-GAN achieves higher predictive performance on all datasets.