Compact Recurrent Transformer with Persistent Memory

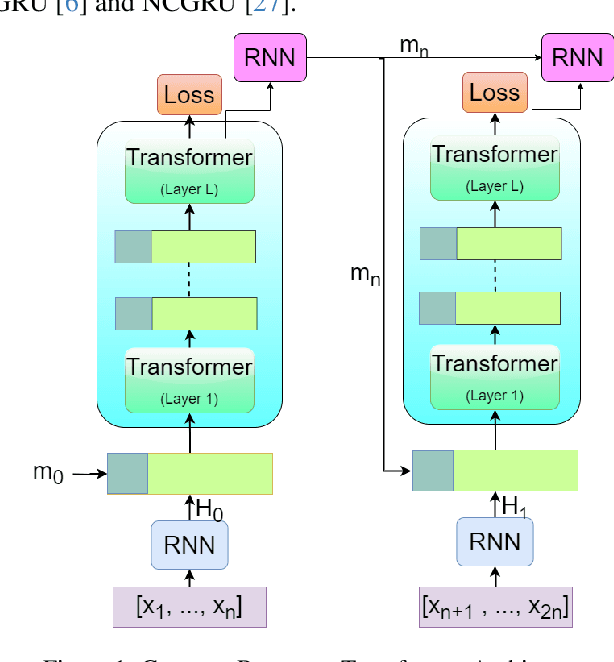
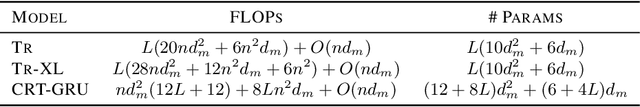
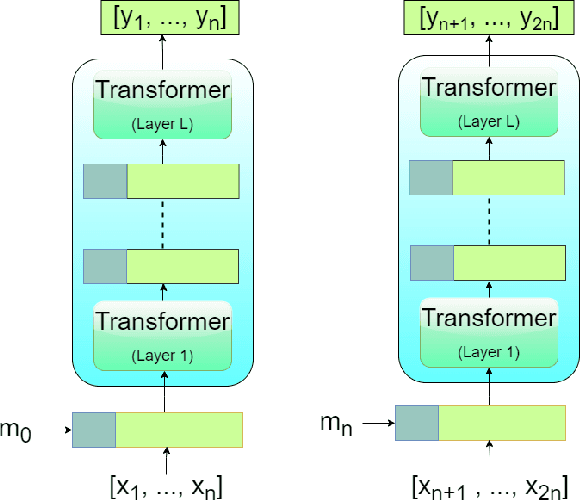
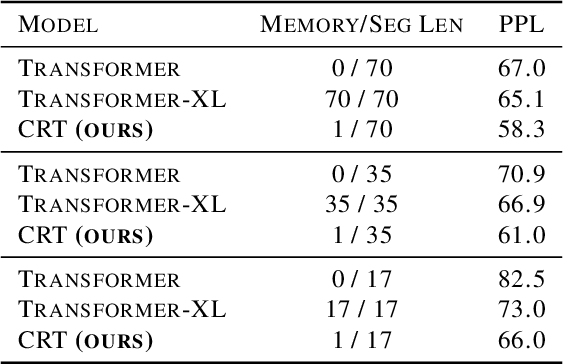
The Transformer architecture has shown significant success in many language processing and visual tasks. However, the method faces challenges in efficiently scaling to long sequences because the self-attention computation is quadratic with respect to the input length. To overcome this limitation, several approaches scale to longer sequences by breaking long sequences into a series of segments, restricting self-attention to local dependencies between tokens within each segment and using a memory mechanism to manage information flow between segments. However, these approached generally introduce additional compute overhead that restricts them from being used for applications where limited compute memory and power are of great concern (such as edge computing). We propose a novel and efficient Compact Recurrent Transformer (CRT), which combines shallow Transformer models that process short local segments with recurrent neural networks to compress and manage a single persistent memory vector that summarizes long-range global information between segments. We evaluate CRT on WordPTB and WikiText-103 for next-token-prediction tasks, as well as on the Toyota Smarthome video dataset for classification. CRT achieves comparable or superior prediction results to full-length Transformers in the language datasets while using significantly shorter segments (half or quarter size) and substantially reduced FLOPs. Our approach also demonstrates state-of-the-art performance on the Toyota Smarthome video dataset.

Noise-Tolerant Coreset-Based Class Incremental Continual Learning

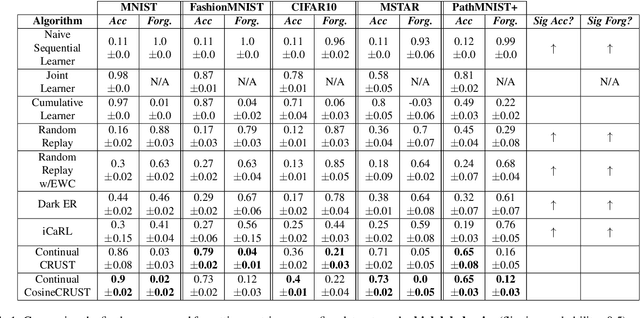
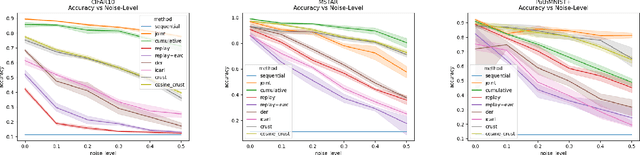
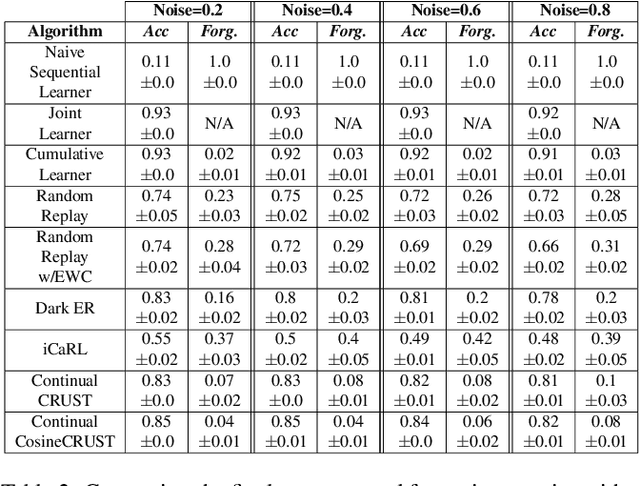
Many applications of computer vision require the ability to adapt to novel data distributions after deployment. Adaptation requires algorithms capable of continual learning (CL). Continual learners must be plastic to adapt to novel tasks while minimizing forgetting of previous tasks.However, CL opens up avenues for noise to enter the training pipeline and disrupt the CL. This work focuses on label noise and instance noise in the context of class-incremental learning (CIL), where new classes are added to a classifier over time, and there is no access to external data from past classes. We aim to understand the sensitivity of CL methods that work by replaying items from a memory constructed using the idea of Coresets. We derive a new bound for the robustness of such a method to uncorrelated instance noise under a general additive noise threat model, revealing several insights. Putting the theory into practice, we create two continual learning algorithms to construct noise-tolerant replay buffers. We empirically compare the effectiveness of prior memory-based continual learners and the proposed algorithms under label and uncorrelated instance noise on five diverse datasets. We show that existing memory-based CL are not robust whereas the proposed methods exhibit significant improvements in maximizing classification accuracy and minimizing forgetting in the noisy CIL setting.

Orthogonal Gated Recurrent Unit with Neumann-Cayley Transformation

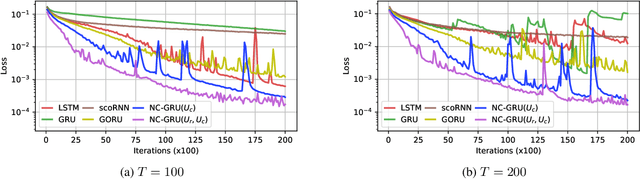
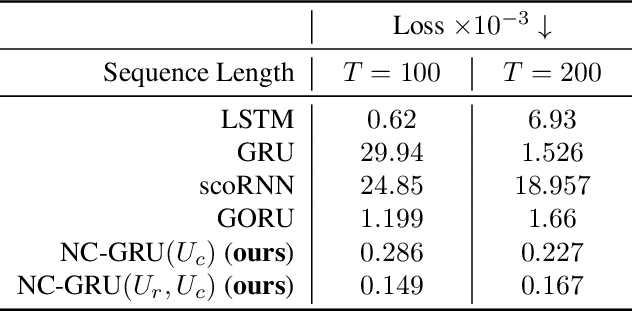
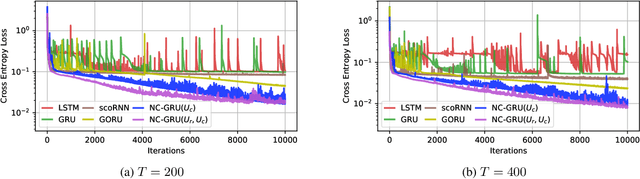
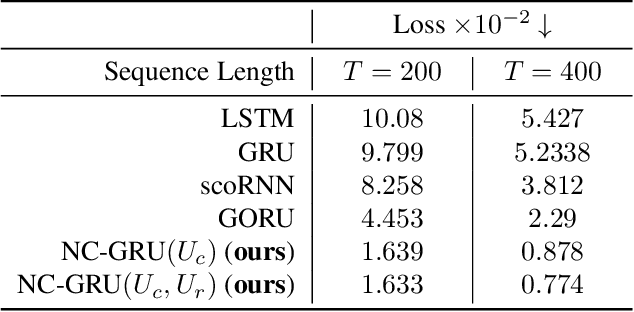
In recent years, using orthogonal matrices has been shown to be a promising approach in improving Recurrent Neural Networks (RNNs) with training, stability, and convergence, particularly, to control gradients. While Gated Recurrent Unit (GRU) and Long Short Term Memory (LSTM) architectures address the vanishing gradient problem by using a variety of gates and memory cells, they are still prone to the exploding gradient problem. In this work, we analyze the gradients in GRU and propose the usage of orthogonal matrices to prevent exploding gradient problems and enhance long-term memory. We study where to use orthogonal matrices and we propose a Neumann series-based Scaled Cayley transformation for training orthogonal matrices in GRU, which we call Neumann-Cayley Orthogonal GRU, or simply NC-GRU. We present detailed experiments of our model on several synthetic and real-world tasks, which show that NC-GRU significantly outperforms GRU as well as several other RNNs.