Breaking Time Invariance: Assorted-Time Normalization for RNNs

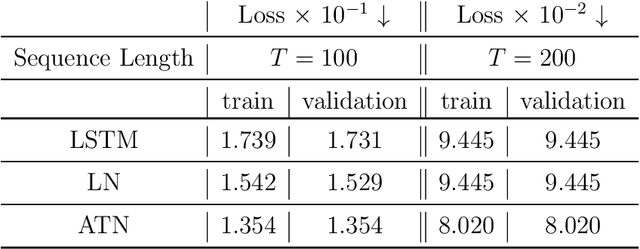
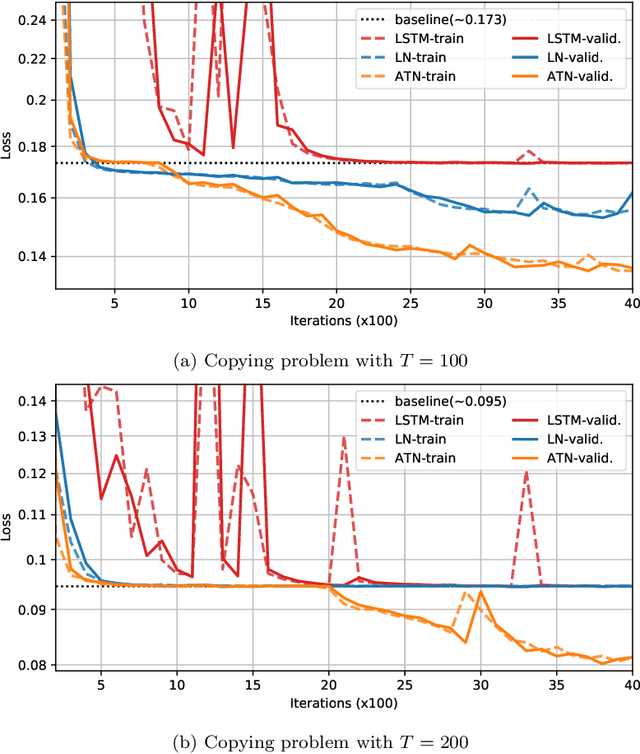
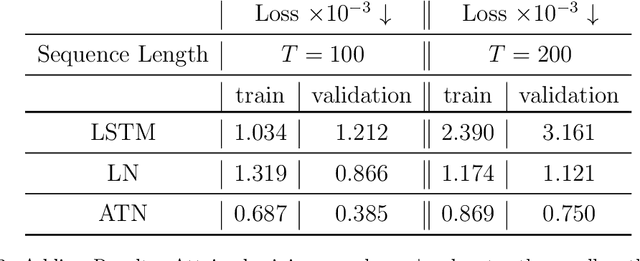
Methods such as Layer Normalization (LN) and Batch Normalization (BN) have proven to be effective in improving the training of Recurrent Neural Networks (RNNs). However, existing methods normalize using only the instantaneous information at one particular time step, and the result of the normalization is a preactivation state with a time-independent distribution. This implementation fails to account for certain temporal differences inherent in the inputs and the architecture of RNNs. Since these networks share weights across time steps, it may also be desirable to account for the connections between time steps in the normalization scheme. In this paper, we propose a normalization method called Assorted-Time Normalization (ATN), which preserves information from multiple consecutive time steps and normalizes using them. This setup allows us to introduce longer time dependencies into the traditional normalization methods without introducing any new trainable parameters. We present theoretical derivations for the gradient propagation and prove the weight scaling invariance property. Our experiments applying ATN to LN demonstrate consistent improvement on various tasks, such as Adding, Copying, and Denoise Problems and Language Modeling Problems.

Orthogonal Gated Recurrent Unit with Neumann-Cayley Transformation

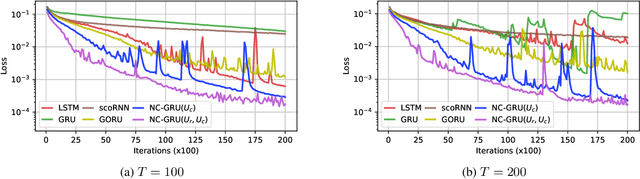
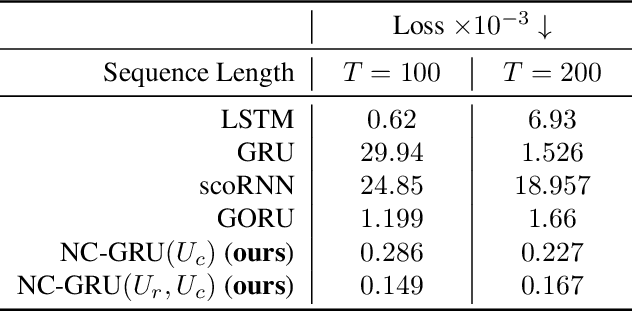
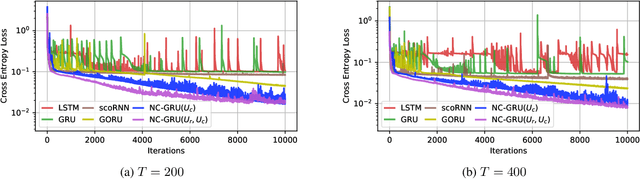
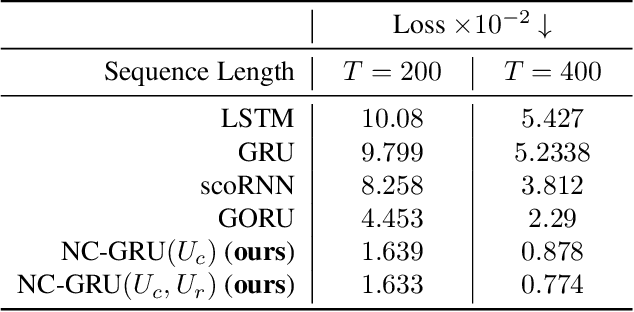
In recent years, using orthogonal matrices has been shown to be a promising approach in improving Recurrent Neural Networks (RNNs) with training, stability, and convergence, particularly, to control gradients. While Gated Recurrent Unit (GRU) and Long Short Term Memory (LSTM) architectures address the vanishing gradient problem by using a variety of gates and memory cells, they are still prone to the exploding gradient problem. In this work, we analyze the gradients in GRU and propose the usage of orthogonal matrices to prevent exploding gradient problems and enhance long-term memory. We study where to use orthogonal matrices and we propose a Neumann series-based Scaled Cayley transformation for training orthogonal matrices in GRU, which we call Neumann-Cayley Orthogonal GRU, or simply NC-GRU. We present detailed experiments of our model on several synthetic and real-world tasks, which show that NC-GRU significantly outperforms GRU as well as several other RNNs.