Eberhard K. A. Gill
Provable Emergent Pattern Formation by a Swarm of Anonymous, Homogeneous, Non-Communicating, Reactive Robots with Limited Relative Sensing and no Global Knowledge or Positioning
Apr 18, 2018


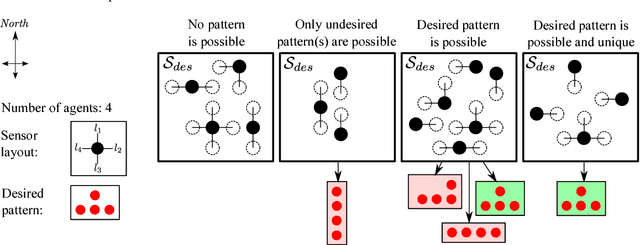
Abstract:In this work, we explore emergent behaviors by swarms of anonymous, homogeneous, non-communicating, reactive robots that do not know their global position and have limited relative sensing. We introduce a novel method that enables such severely limited robots to autonomously arrange in a desired pattern and maintain it. The method includes an automatic proof procedure to check whether a given pattern will be achieved by the swarm from any initial configuration. An attractive feature of this proof procedure is that it is local in nature, avoiding as much as possible the computational explosion that can be expected with increasing robots, states, and action possibilities. Our approach is based on extracting the local states that constitute a global goal (in this case, a pattern). We then formally show that these local states can only coexist when the global desired pattern is achieved and that, until this occurs, there is always a sequence of actions that will lead from the current pattern to the desired pattern. Furthermore, we show that the agents will never perform actions that could a) lead to intra-swarm collisions or b) cause the swarm to separate. After an analysis of the performance of pattern formation in the discrete domain, we also test the system in continuous time and space simulations and reproduce the results using asynchronous agents operating in unbounded space. The agents successfully form the desired patterns while avoiding collisions and separation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge