RNN-Based GNSS Positioning using Satellite Measurement Features and Pseudorange Residuals

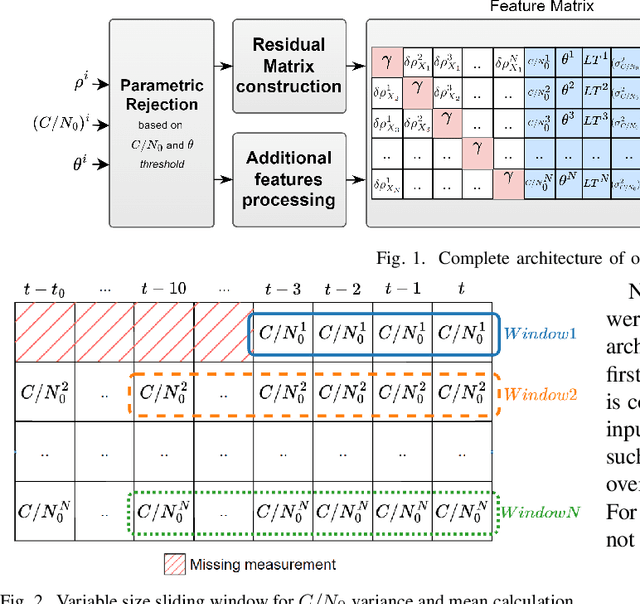
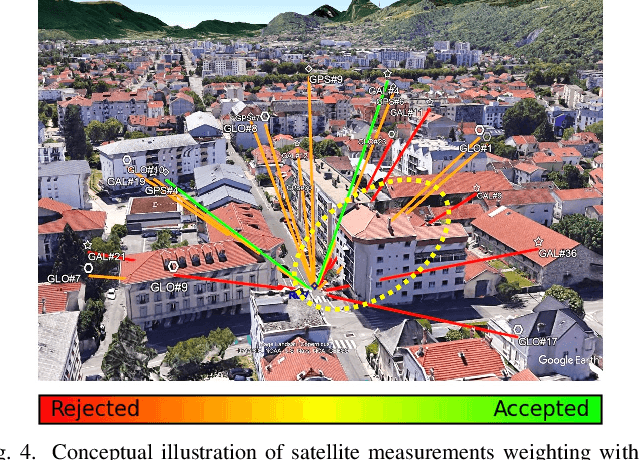
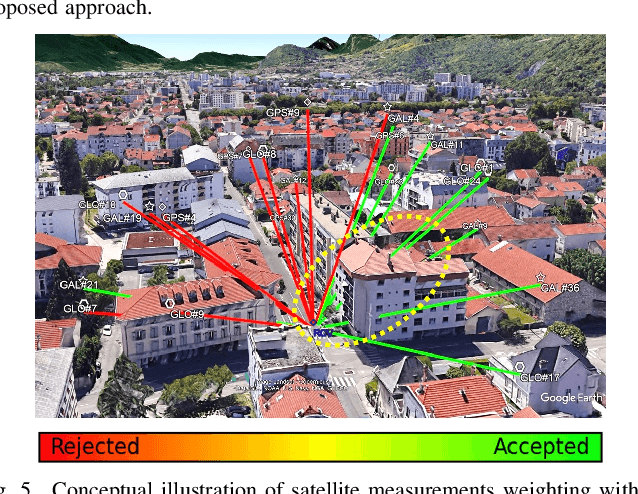
In the Global Navigation Satellite System (GNSS) context, the growing number of available satellites has lead to many challenges when it comes to choosing the most accurate pseudorange contributions, given the strong impact of biased measurements on positioning accuracy, particularly in single-epoch scenarios. This work leverages the potential of machine learning in predicting link-wise measurement quality factors and, hence, optimize measurement weighting. For this purpose, we use a customized matrix composed of heterogeneous features such as conditional pseudorange residuals and per-link satellite metrics (e.g., carrier-to-noise power density ratio and its empirical statistics, satellite elevation, carrier phase lock time). This matrix is then fed as an input to a recurrent neural network (RNN) (i.e., a long-short term memory (LSTM) network). Our experimental results on real data, obtained from extensive field measurements, demonstrate the high potential of our proposed solution being able to outperform traditional measurements weighting and selection strategies from state-of-the-art.

Adaptive extra-gradient methods for min-max optimization and games

We present a new family of min-max optimization algorithms that automatically exploit the geometry of the gradient data observed at earlier iterations to perform more informative extra-gradient steps in later ones. Thanks to this adaptation mechanism, the proposed methods automatically detect the problem's smoothness properties, without requiring any prior tuning by the optimizer. As a result, the algorithm simultaneously achieves the optimal smooth/non-smooth min-max convergence rates, i.e., it converges to an $\varepsilon$-optimal solution within $\mathcal{O}(1/\varepsilon)$ iterations in smooth problems, and within $\mathcal{O}(1/\varepsilon^2)$ iterations in non-smooth ones. Importantly, these guarantees do not require any of the standard boundedness or Lipschitz continuity conditions that are typically assumed in the literature; in particular, they apply even to problems with divergent loss functions (such as log-likelihood learning and the like). This "off-the-shelf" adaptation is achieved through the use of a geometric apparatus based on Finsler metrics and a suitably chosen mirror-prox template that allows us to derive sharp convergence rates for the family of methods at hand.

Online convex optimization and no-regret learning: Algorithms, guarantees and applications

Spurred by the enthusiasm surrounding the "Big Data" paradigm, the mathematical and algorithmic tools of online optimization have found widespread use in problems where the trade-off between data exploration and exploitation plays a predominant role. This trade-off is of particular importance to several branches and applications of signal processing, such as data mining, statistical inference, multimedia indexing and wireless communications (to name but a few). With this in mind, the aim of this tutorial paper is to provide a gentle introduction to online optimization and learning algorithms that are asymptotically optimal in hindsight - i.e., they approach the performance of a virtual algorithm with unlimited computational power and full knowledge of the future, a property known as no-regret. Particular attention is devoted to identifying the algorithms' theoretical performance guarantees and to establish links with classic optimization paradigms (both static and stochastic). To allow a better understanding of this toolbox, we provide several examples throughout the tutorial ranging from metric learning to wireless resource allocation problems.

Distributed stochastic optimization via matrix exponential learning

In this paper, we investigate a distributed learning scheme for a broad class of stochastic optimization problems and games that arise in signal processing and wireless communications. The proposed algorithm relies on the method of matrix exponential learning (MXL) and only requires locally computable gradient observations that are possibly imperfect and/or obsolete. To analyze it, we introduce the notion of a stable Nash equilibrium and we show that the algorithm is globally convergent to such equilibria - or locally convergent when an equilibrium is only locally stable. We also derive an explicit linear bound for the algorithm's convergence speed, which remains valid under measurement errors and uncertainty of arbitrarily high variance. To validate our theoretical analysis, we test the algorithm in realistic multi-carrier/multiple-antenna wireless scenarios where several users seek to maximize their energy efficiency. Our results show that learning allows users to attain a net increase between 100% and 500% in energy efficiency, even under very high uncertainty.