E. Rougier
Estimating Failure in Brittle Materials using Graph Theory
Jul 30, 2018
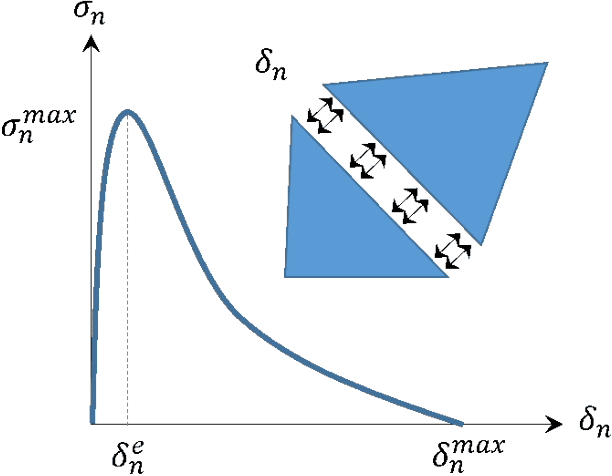
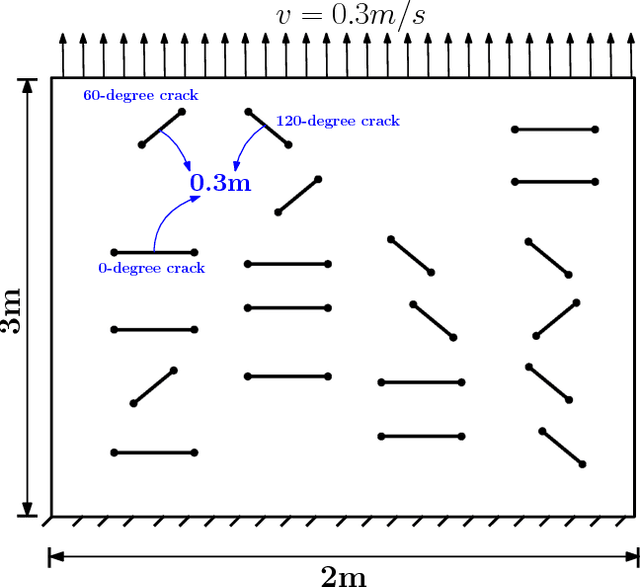
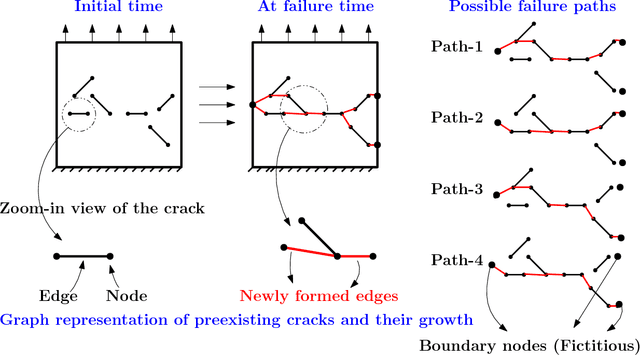
Abstract:In brittle fracture applications, failure paths, regions where the failure occurs and damage statistics, are some of the key quantities of interest (QoI). High-fidelity models for brittle failure that accurately predict these QoI exist but are highly computationally intensive, making them infeasible to incorporate in upscaling and uncertainty quantification frameworks. The goal of this paper is to provide a fast heuristic to reasonably estimate quantities such as failure path and damage in the process of brittle failure. Towards this goal, we first present a method to predict failure paths under tensile loading conditions and low-strain rates. The method uses a $k$-nearest neighbors algorithm built on fracture process zone theory, and identifies the set of all possible pre-existing cracks that are likely to join early to form a large crack. The method then identifies zone of failure and failure paths using weighted graphs algorithms. We compare these failure paths to those computed with a high-fidelity model called the Hybrid Optimization Software Simulation Suite (HOSS). A probabilistic evolution model for average damage in a system is also developed that is trained using 150 HOSS simulations and tested on 40 simulations. A non-parametric approach based on confidence intervals is used to determine the damage evolution over time along the dominant failure path. For upscaling, damage is the key QoI needed as an input by the continuum models. This needs to be informed accurately by the surrogate models for calculating effective modulii at continuum-scale. We show that for the proposed average damage evolution model, the prediction accuracy on the test data is more than 90\%. In terms of the computational time, the proposed models are $\approx \mathcal{O}(10^6)$ times faster compared to high-fidelity HOSS.
Reduced-Order Modeling through Machine Learning Approaches for Brittle Fracture Applications
Jun 05, 2018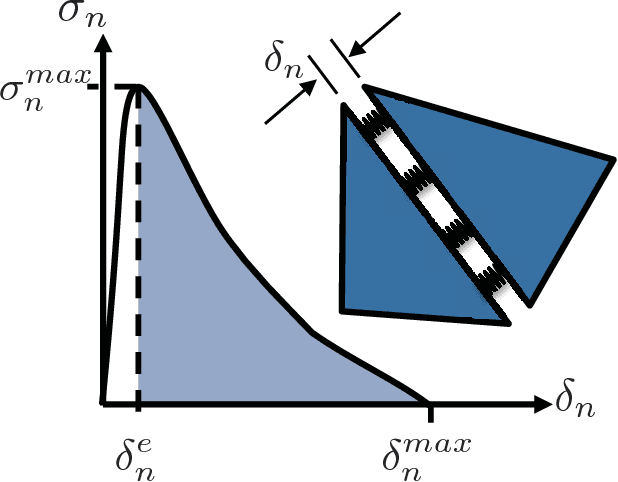
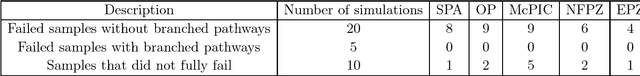

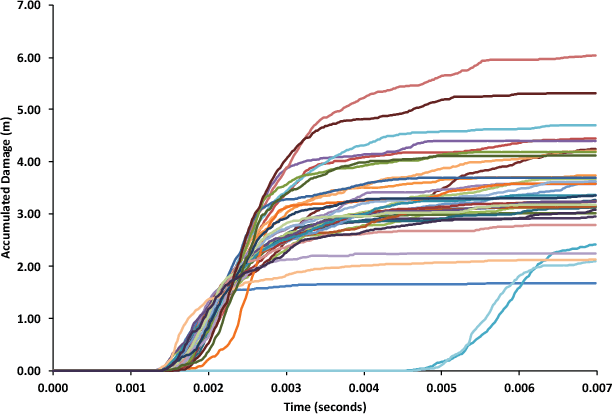
Abstract:In this paper, five different approaches for reduced-order modeling of brittle fracture in geomaterials, specifically concrete, are presented and compared. Four of the five methods rely on machine learning (ML) algorithms to approximate important aspects of the brittle fracture problem. In addition to the ML algorithms, each method incorporates different physics-based assumptions in order to reduce the computational complexity while maintaining the physics as much as possible. This work specifically focuses on using the ML approaches to model a 2D concrete sample under low strain rate pure tensile loading conditions with 20 preexisting cracks present. A high-fidelity finite element-discrete element model is used to both produce a training dataset of 150 simulations and an additional 35 simulations for validation. Results from the ML approaches are directly compared against the results from the high-fidelity model. Strengths and weaknesses of each approach are discussed and the most important conclusion is that a combination of physics-informed and data-driven features are necessary for emulating the physics of crack propagation, interaction and coalescence. All of the models presented here have runtimes that are orders of magnitude faster than the original high-fidelity model and pave the path for developing accurate reduced order models that could be used to inform larger length-scale models with important sub-scale physics that often cannot be accounted for due to computational cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge