E. Garone
Self-organizing Nervous Systems for Robot Swarms
Jan 23, 2024Abstract:The system architecture controlling a group of robots is generally set before deployment and can be either centralized or decentralized. This dichotomy is highly constraining, because decentralized systems are typically fully self-organized and therefore difficult to design analytically, whereas centralized systems have single points of failure and limited scalability. To address this dichotomy, we present the Self-organizing Nervous System (SoNS), a novel robot swarm architecture based on self-organized hierarchy. The SoNS approach enables robots to autonomously establish, maintain, and reconfigure dynamic multi-level system architectures. For example, a robot swarm consisting of $n$ independent robots could transform into a single $n$-robot SoNS and then into several independent smaller SoNSs, where each SoNS uses a temporary and dynamic hierarchy. Leveraging the SoNS approach, we show that sensing, actuation, and decision-making can be coordinated in a locally centralized way, without sacrificing the benefits of scalability, flexibility, and fault tolerance, for which swarm robotics is usually studied. In several proof-of-concept robot missions -- including binary decision-making and search-and-rescue -- we demonstrate that the capabilities of the SoNS approach greatly advance the state of the art in swarm robotics. The missions are conducted with a real heterogeneous aerial-ground robot swarm, using a custom-developed quadrotor platform. We also demonstrate the scalability of the SoNS approach in swarms of up to 250 robots in a physics-based simulator, and demonstrate several types of system fault tolerance in simulation and reality.
Modelling and Control of a Knuckle Boom Crane
Mar 30, 2021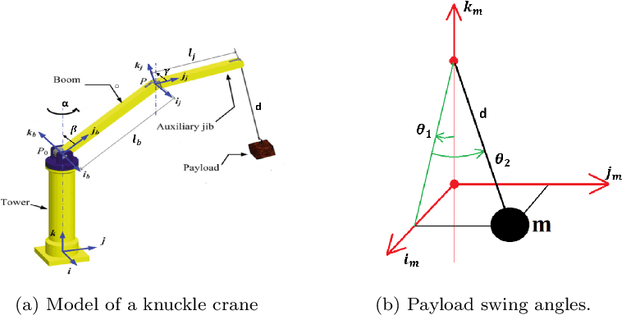



Abstract:Cranes come in various sizes and designs to perform different tasks. Depending on their dynamic properties, they can be classified as gantry cranes and rotary cranes. In this paper we will focus on the so called 'knuckle boom' cranes which are among the most common types of rotary cranes. Compared with the other kinds of cranes (e.g. boom cranes, tower cranes, overhead cranes, etc), the study of knuckle cranes is still at an early stage and very few control strategies for this kind of crane have been proposed in the literature. Although fairly simple mechanically, from the control viewpoint the knuckle cranes present several challenges. A first result of this paper is to present for the first time a complete mathematical model for this kind of crane where it is possible to control the three rotations of the crane (known as luff, slew, and jib movement), and the cable length. The only simplifying assumption of the model is that the cable is considered rigid. On the basis of this model, we propose a nonlinear control law based on energy considerations which is able to perform position control of the crane while actively damping the oscillations of the load. The corresponding stability and convergence analysis is carefully proved using the LaSalle's invariance principle. The effectiveness of the proposed control approach has been tested in simulation with realistic physical parameters and in the presence of model mismatch.
* This paper has been accepted to International Journal of Control on March 29th 2021. arXiv admin note: text overlap with arXiv:2103.02509
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge