Modelling and Control of a Knuckle Boom Crane
Paper and Code
Mar 30, 2021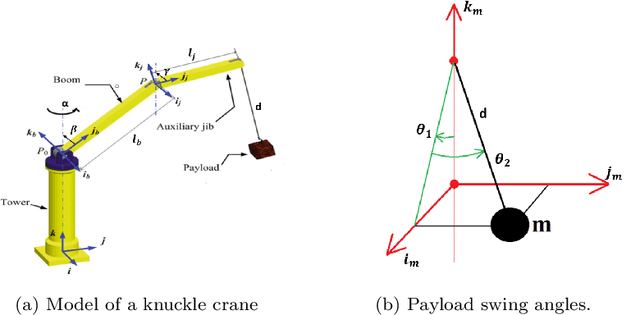



Cranes come in various sizes and designs to perform different tasks. Depending on their dynamic properties, they can be classified as gantry cranes and rotary cranes. In this paper we will focus on the so called 'knuckle boom' cranes which are among the most common types of rotary cranes. Compared with the other kinds of cranes (e.g. boom cranes, tower cranes, overhead cranes, etc), the study of knuckle cranes is still at an early stage and very few control strategies for this kind of crane have been proposed in the literature. Although fairly simple mechanically, from the control viewpoint the knuckle cranes present several challenges. A first result of this paper is to present for the first time a complete mathematical model for this kind of crane where it is possible to control the three rotations of the crane (known as luff, slew, and jib movement), and the cable length. The only simplifying assumption of the model is that the cable is considered rigid. On the basis of this model, we propose a nonlinear control law based on energy considerations which is able to perform position control of the crane while actively damping the oscillations of the load. The corresponding stability and convergence analysis is carefully proved using the LaSalle's invariance principle. The effectiveness of the proposed control approach has been tested in simulation with realistic physical parameters and in the presence of model mismatch.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge