Modeling Spatial Extremes using Non-Gaussian Spatial Autoregressive Models via Convolutional Neural Networks

Data derived from remote sensing or numerical simulations often have a regular gridded structure and are large in volume, making it challenging to find accurate spatial models that can fill in missing grid cells or simulate the process effectively, especially in the presence of spatial heterogeneity and heavy-tailed marginal distributions. To overcome this issue, we present a spatial autoregressive modeling framework, which maps observations at a location and its neighbors to independent random variables. This is a highly flexible modeling approach and well-suited for non-Gaussian fields, providing simpler interpretability. In particular, we consider the SAR model with Generalized Extreme Value distribution innovations to combine the observation at a central grid location with its neighbors, capturing extreme spatial behavior based on the heavy-tailed innovations. While these models are fast to simulate by exploiting the sparsity of the key matrices in the computations, the maximum likelihood estimation of the parameters is prohibitive due to the intractability of the likelihood, making optimization challenging. To overcome this, we train a convolutional neural network on a large training set that covers a useful parameter space, and then use the trained network for fast parameter estimation. Finally, we apply this model to analyze annual maximum precipitation data from ERA-Interim-driven Weather Research and Forecasting (WRF) simulations, allowing us to explore its spatial extreme behavior across North America.

Fast parameter estimation of Generalized Extreme Value distribution using Neural Networks

The heavy-tailed behavior of the generalized extreme-value distribution makes it a popular choice for modeling extreme events such as floods, droughts, heatwaves, wildfires, etc. However, estimating the distribution's parameters using conventional maximum likelihood methods can be computationally intensive, even for moderate-sized datasets. To overcome this limitation, we propose a computationally efficient, likelihood-free estimation method utilizing a neural network. Through an extensive simulation study, we demonstrate that the proposed neural network-based method provides Generalized Extreme Value (GEV) distribution parameter estimates with comparable accuracy to the conventional maximum likelihood method but with a significant computational speedup. To account for estimation uncertainty, we utilize parametric bootstrapping, which is inherent in the trained network. Finally, we apply this method to 1000-year annual maximum temperature data from the Community Climate System Model version 3 (CCSM3) across North America for three atmospheric concentrations: 289 ppm $\mathrm{CO}_2$ (pre-industrial), 700 ppm $\mathrm{CO}_2$ (future conditions), and 1400 ppm $\mathrm{CO}_2$, and compare the results with those obtained using the maximum likelihood approach.

Fast covariance parameter estimation of spatial Gaussian process models using neural networks

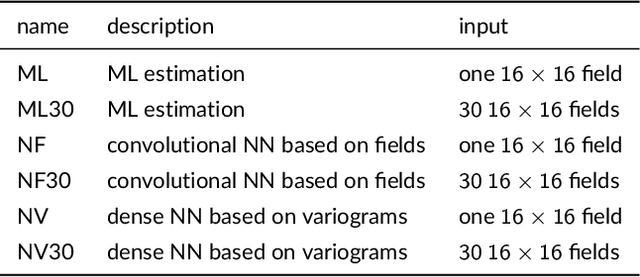
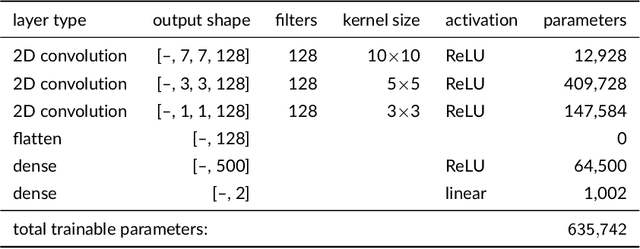
Gaussian processes (GPs) are a popular model for spatially referenced data and allow descriptive statements, predictions at new locations, and simulation of new fields. Often a few parameters are sufficient to parameterize the covariance function, and maximum likelihood (ML) methods can be used to estimate these parameters from data. ML methods, however, are computationally demanding. For example, in the case of local likelihood estimation, even fitting covariance models on modest size windows can overwhelm typical computational resources for data analysis. This limitation motivates the idea of using neural network (NN) methods to approximate ML estimates. We train NNs to take moderate size spatial fields or variograms as input and return the range and noise-to-signal covariance parameters. Once trained, the NNs provide estimates with a similar accuracy compared to ML estimation and at a speedup by a factor of 100 or more. Although we focus on a specific covariance estimation problem motivated by a climate science application, this work can be easily extended to other, more complex, spatial problems and provides a proof-of-concept for this use of machine learning in computational statistics.