Fast covariance parameter estimation of spatial Gaussian process models using neural networks
Paper and Code
Dec 30, 2020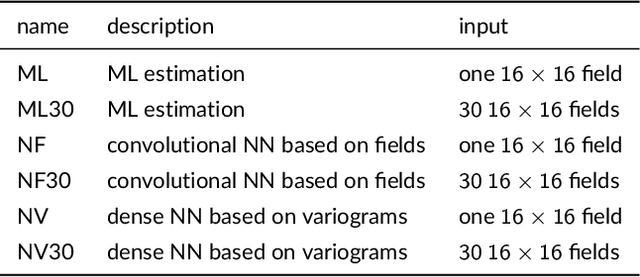

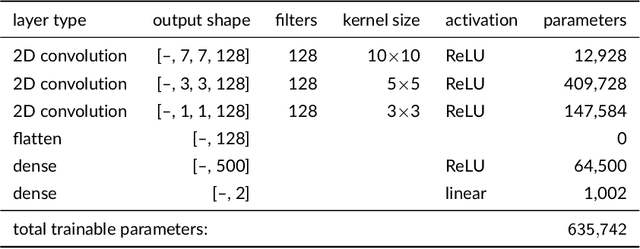

Gaussian processes (GPs) are a popular model for spatially referenced data and allow descriptive statements, predictions at new locations, and simulation of new fields. Often a few parameters are sufficient to parameterize the covariance function, and maximum likelihood (ML) methods can be used to estimate these parameters from data. ML methods, however, are computationally demanding. For example, in the case of local likelihood estimation, even fitting covariance models on modest size windows can overwhelm typical computational resources for data analysis. This limitation motivates the idea of using neural network (NN) methods to approximate ML estimates. We train NNs to take moderate size spatial fields or variograms as input and return the range and noise-to-signal covariance parameters. Once trained, the NNs provide estimates with a similar accuracy compared to ML estimation and at a speedup by a factor of 100 or more. Although we focus on a specific covariance estimation problem motivated by a climate science application, this work can be easily extended to other, more complex, spatial problems and provides a proof-of-concept for this use of machine learning in computational statistics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge