PCCC: The Pairwise-Confidence-Constraints-Clustering Algorithm

We consider a semi-supervised $k$-clustering problem where information is available on whether pairs of objects are in the same or in different clusters. This information is either available with certainty or with a limited level of confidence. We introduce the PCCC algorithm, which iteratively assigns objects to clusters while accounting for the information provided on the pairs of objects. Our algorithm can include relationships as hard constraints that are guaranteed to be satisfied or as soft constraints that can be violated subject to a penalty. This flexibility distinguishes our algorithm from the state-of-the-art in which all pairwise constraints are either considered hard, or all are considered soft. Unlike existing algorithms, our algorithm scales to large-scale instances with up to 60,000 objects, 100 clusters, and millions of cannot-link constraints (which are the most challenging constraints to incorporate). We compare the PCCC algorithm with state-of-the-art approaches in an extensive computational study. Even though the PCCC algorithm is more general than the state-of-the-art approaches in its applicability, it outperforms the state-of-the-art approaches on instances with all hard constraints or all soft constraints both in terms of running time and various metrics of solution quality. The source code of the PCCC algorithm is publicly available on GitHub.

Joint aggregation of cardinal and ordinal evaluations with an application to a student paper competition

An important problem in decision theory concerns the aggregation of individual rankings/ratings into a collective evaluation. We illustrate a new aggregation method in the context of the 2007 MSOM's student paper competition. The aggregation problem in this competition poses two challenges. Firstly, each paper was reviewed only by a very small fraction of the judges; thus the aggregate evaluation is highly sensitive to the subjective scales chosen by the judges. Secondly, the judges provided both cardinal and ordinal evaluations (ratings and rankings) of the papers they reviewed. The contribution here is a new robust methodology that jointly aggregates ordinal and cardinal evaluations into a collective evaluation. This methodology is particularly suitable in cases of incomplete evaluations -- i.e., when the individuals evaluate only a strict subset of the objects. This approach is potentially useful in managerial decision making problems by a committee selecting projects from a large set or capital budgeting involving multiple priorities.

The Max-Cut Decision Tree: Improving on the Accuracy and Running Time of Decision Trees

Decision trees are a widely used method for classification, both by themselves and as the building blocks of multiple different ensemble learning methods. The Max-Cut decision tree involves novel modifications to a standard, baseline model of classification decision tree construction, precisely CART Gini. One modification involves an alternative splitting metric, maximum cut, based on maximizing the distance between all pairs of observations belonging to separate classes and separate sides of the threshold value. The other modification is to select the decision feature from a linear combination of the input features constructed using Principal Component Analysis (PCA) locally at each node. Our experiments show that this node-based localized PCA with the novel splitting modification can dramatically improve classification, while also significantly decreasing computational time compared to the baseline decision tree. Moreover, our results are most significant when evaluated on data sets with higher dimensions, or more classes; which, for the example data set CIFAR-100, enable a 49% improvement in accuracy while reducing CPU time by 94%. These introduced modifications dramatically advance the capabilities of decision trees for difficult classification tasks.

Competitive Analysis of Minimum-Cut Maximum Flow Algorithms in Vision Problems

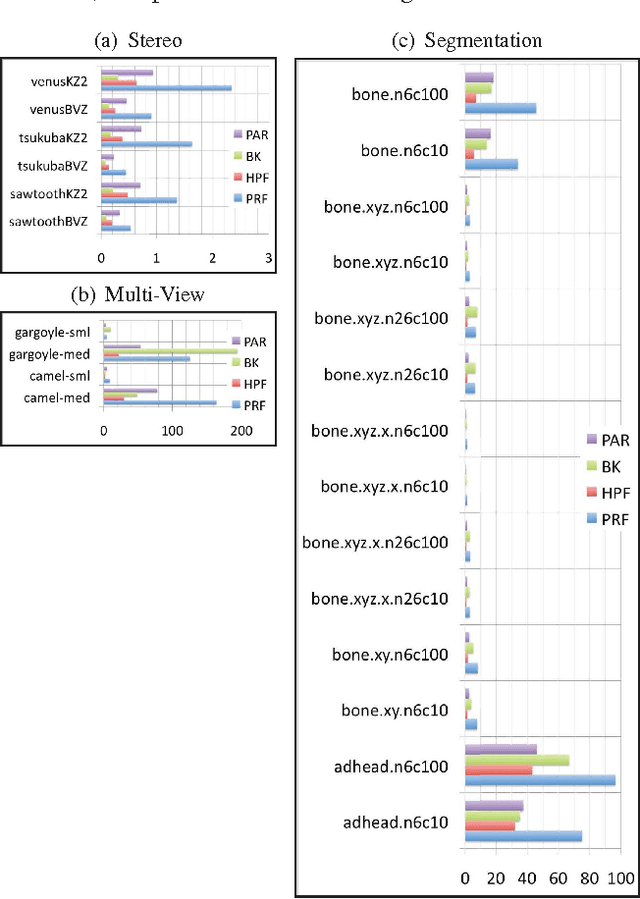
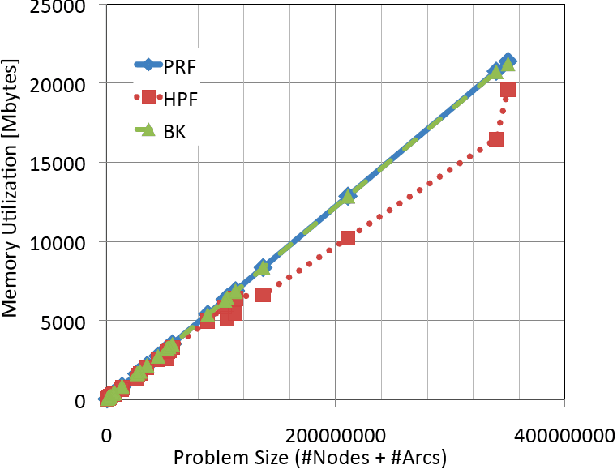
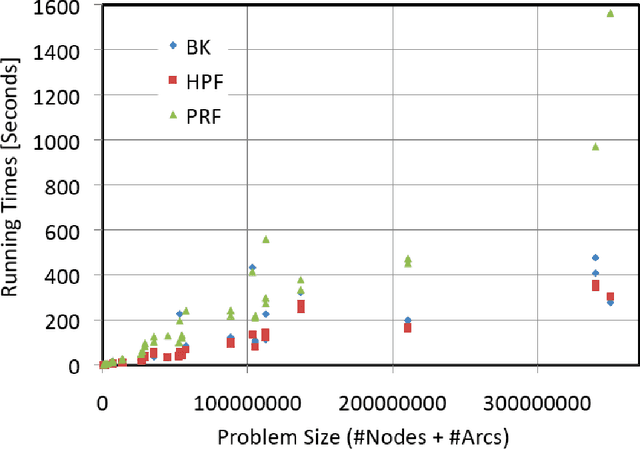
Rapid advances in image acquisition and storage technology underline the need for algorithms that are capable of solving large scale image processing and computer-vision problems. The minimum cut problem plays an important role in processing many of these imaging problems such as, image and video segmentation, stereo vision, multi-view reconstruction and surface fitting. While several min-cut/max-flow algorithms can be found in the literature, their performance in practice has been studied primarily outside the scope of computer vision. We present here the results of a comprehensive computational study, in terms of execution times and memory utilization, of four recently published algorithms, which optimally solve the {\em s-t} cut and maximum flow problems: (i) Goldberg's and Tarjan's {\em Push-Relabel}; (ii) Hochbaum's {\em pseudoflow}; (iii) Boykov's and Kolmogorov's {\em augmenting paths}; and (iv) Goldberg's {\em partial augment-relabel}. Our results demonstrate that the {\em Hochbaum's pseudoflow} algorithm, is faster and utilizes less memory than the other algorithms on all problem instances investigated.

Polynomial time algorithms for bi-criteria, multi-objective and ratio problems in clustering and imaging. Part I: Normalized cut and ratio regions

Partitioning and grouping of similar objects plays a fundamental role in image segmentation and in clustering problems. In such problems a typical goal is to group together similar objects, or pixels in the case of image processing. At the same time another goal is to have each group distinctly dissimilar from the rest and possibly to have the group size fairly large. These goals are often combined as a ratio optimization problem. One example of such problem is the normalized cut problem, another is the ratio regions problem. We devise here the first polynomial time algorithms solving these problems optimally. The algorithms are efficient and combinatorial. This contrasts with the heuristic approaches used in the image segmentation literature that formulate those problems as nonlinear optimization problems, which are then relaxed and solved with spectral techniques in real numbers. These approaches not only fail to deliver an optimal solution, but they are also computationally expensive. The algorithms presented here use as a subroutine a minimum $s,t-cut procedure on a related graph which is of polynomial size. The output consists of the optimal solution to the respective ratio problem, as well as a sequence of nested solution with respect to any relative weighting of the objectives of the numerator and denominator. An extension of the results here to bi-criteria and multi-criteria objective functions is presented in part II.