Competitive Analysis of Minimum-Cut Maximum Flow Algorithms in Vision Problems
Paper and Code
Oct 18, 2010
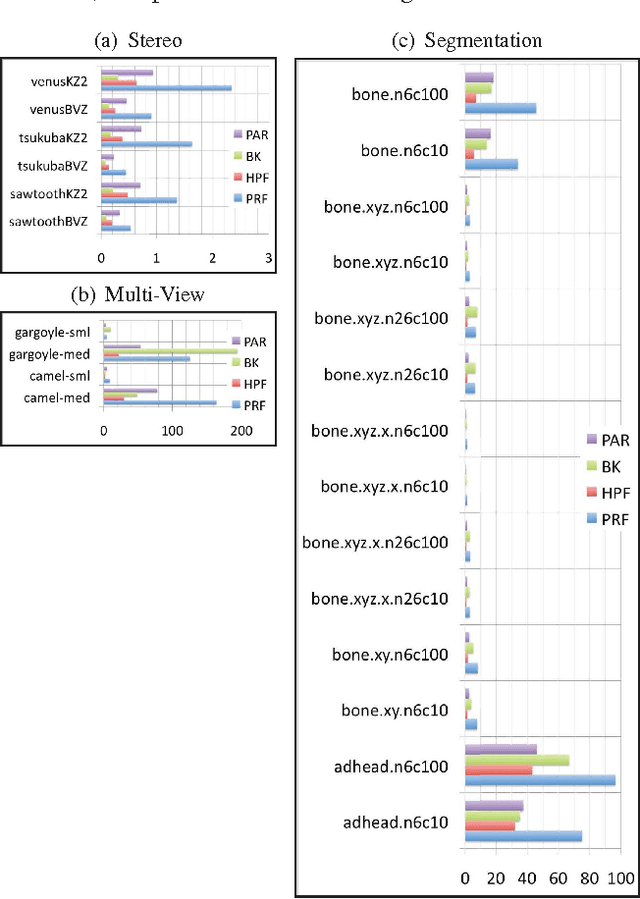
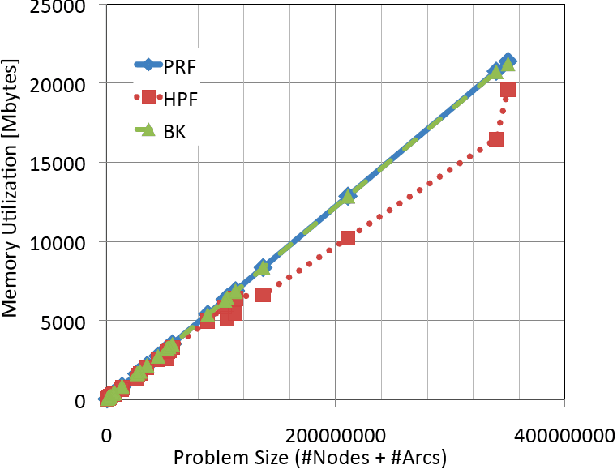
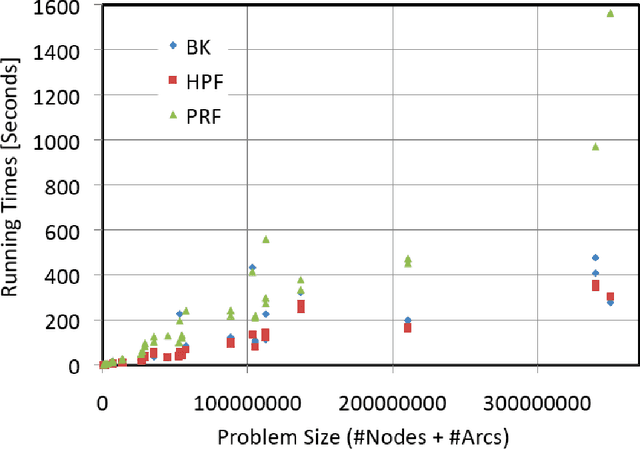
Rapid advances in image acquisition and storage technology underline the need for algorithms that are capable of solving large scale image processing and computer-vision problems. The minimum cut problem plays an important role in processing many of these imaging problems such as, image and video segmentation, stereo vision, multi-view reconstruction and surface fitting. While several min-cut/max-flow algorithms can be found in the literature, their performance in practice has been studied primarily outside the scope of computer vision. We present here the results of a comprehensive computational study, in terms of execution times and memory utilization, of four recently published algorithms, which optimally solve the {\em s-t} cut and maximum flow problems: (i) Goldberg's and Tarjan's {\em Push-Relabel}; (ii) Hochbaum's {\em pseudoflow}; (iii) Boykov's and Kolmogorov's {\em augmenting paths}; and (iv) Goldberg's {\em partial augment-relabel}. Our results demonstrate that the {\em Hochbaum's pseudoflow} algorithm, is faster and utilizes less memory than the other algorithms on all problem instances investigated.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge