Polarimetric BSSRDF Acquisition of Dynamic Faces

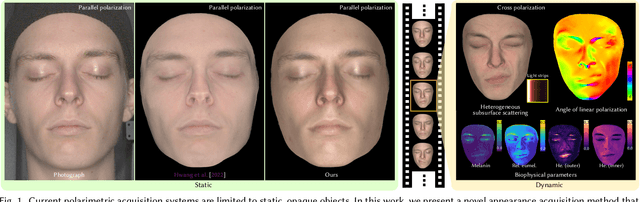
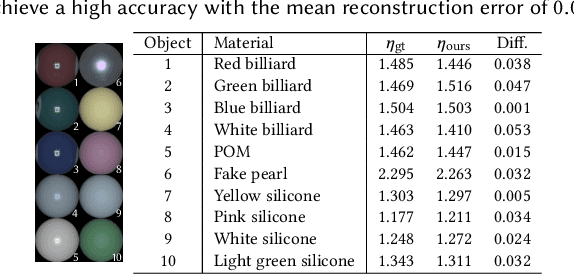
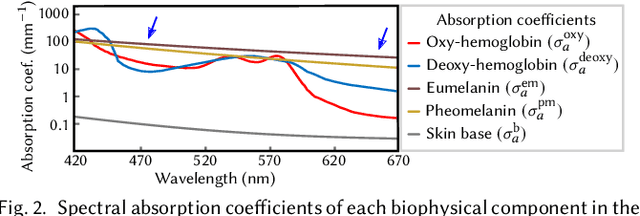
Acquisition and modeling of polarized light reflection and scattering help reveal the shape, structure, and physical characteristics of an object, which is increasingly important in computer graphics. However, current polarimetric acquisition systems are limited to static and opaque objects. Human faces, on the other hand, present a particularly difficult challenge, given their complex structure and reflectance properties, the strong presence of spatially-varying subsurface scattering, and their dynamic nature. We present a new polarimetric acquisition method for dynamic human faces, which focuses on capturing spatially varying appearance and precise geometry, across a wide spectrum of skin tones and facial expressions. It includes both single and heterogeneous subsurface scattering, index of refraction, and specular roughness and intensity, among other parameters, while revealing biophysically-based components such as inner- and outer-layer hemoglobin, eumelanin and pheomelanin. Our method leverages such components' unique multispectral absorption profiles to quantify their concentrations, which in turn inform our model about the complex interactions occurring within the skin layers. To our knowledge, our work is the first to simultaneously acquire polarimetric and spectral reflectance information alongside biophysically-based skin parameters and geometry of dynamic human faces. Moreover, our polarimetric skin model integrates seamlessly into various rendering pipelines.

PCA, SVD, and Centering of Data

The research detailed in this paper scrutinizes Principal Component Analysis (PCA), a seminal method employed in statistics and machine learning for the purpose of reducing data dimensionality. Singular Value Decomposition (SVD) is often employed as the primary means for computing PCA, a process that indispensably includes the step of centering - the subtraction of the mean location from the data set. In our study, we delve into a detailed exploration of the influence of this critical yet often ignored or downplayed data centering step. Our research meticulously investigates the conditions under which two PCA embeddings, one derived from SVD with centering and the other without, can be viewed as aligned. As part of this exploration, we analyze the relationship between the first singular vector and the mean direction, subsequently linking this observation to the congruity between two SVDs of centered and uncentered matrices. Furthermore, we explore the potential implications arising from the absence of centering in the context of performing PCA via SVD from a spectral analysis standpoint. Our investigation emphasizes the importance of a comprehensive understanding and acknowledgment of the subtleties involved in the computation of PCA. As such, we believe this paper offers a crucial contribution to the nuanced understanding of this foundational statistical method and stands as a valuable addition to the academic literature in the field of statistics.