Morphological segmentation of hyperspectral images

The present paper develops a general methodology for the morphological segmentation of hyperspectral images, i.e., with an important number of channels. This approach, based on watershed, is composed of a spectral classification to obtain the markers and a vectorial gradient which gives the spatial information. Several alternative gradients are adapted to the different hyperspectral functions. Data reduction is performed either by Factor Analysis or by model fitting. Image segmentation is done on different spaces: factor space, parameters space, etc. On all these spaces the spatial/spectral segmentation approach is applied, leading to relevant results on the image.

Multivariate mathematical morphology for DCE-MRI image analysis in angiogenesis studies

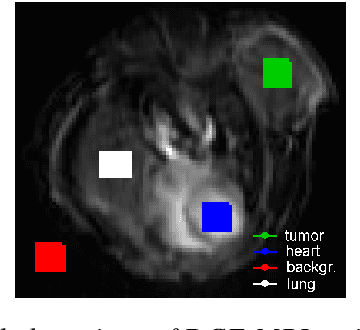
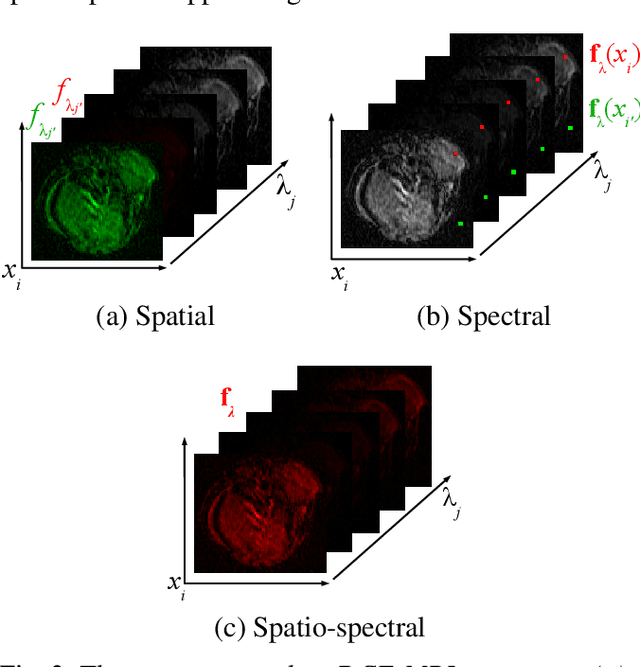
We propose a new computer aided detection framework for tumours acquired on DCE-MRI (Dynamic Contrast Enhanced Magnetic Resonance Imaging) series on small animals. In this approach we consider DCE-MRI series as multivariate images. A full multivariate segmentation method based on dimensionality reduction, noise filtering, supervised classification and stochastic watershed is explained and tested on several data sets. The two main key-points introduced in this paper are noise reduction preserving contours and spatio temporal segmentation by stochastic watershed. Noise reduction is performed in a special way that selects factorial axes of Factor Correspondence Analysis in order to preserves contours. Then a spatio-temporal approach based on stochastic watershed is used to segment tumours. The results obtained are in accordance with the diagnosis of the medical doctors.

A New Spatio-Spectral Morphological Segmentation For Multi-Spectral Remote-Sensing Images

A general framework of spatio-spectral segmentation for multi-spectral images is introduced in this paper. The method is based on classification-driven stochastic watershed (WS) by Monte Carlo simulations, and it gives more regular and reliable contours than standard WS. The present approach is decomposed into several sequential steps. First, a dimensionality-reduction stage is performed using the factor-correspondence analysis method. In this context, a new way to select the factor axes (eigenvectors) according to their spatial information is introduced. Then, a spectral classification produces a spectral pre-segmentation of the image. Subsequently, a probability density function (pdf) of contours containing spatial and spectral information is estimated by simulation using a stochastic WS approach driven by the spectral classification. The pdf of the contours is finally segmented by a WS controlled by markers from a regularization of the initial classification.

On distances, paths and connections for hyperspectral image segmentation

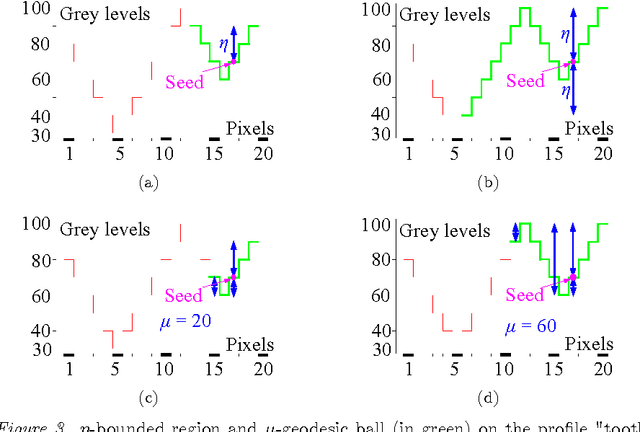
The present paper introduces the $\eta$ and {\eta} connections in order to add regional information on $\lambda$-flat zones, which only take into account a local information. A top-down approach is considered. First $\lambda$-flat zones are built in a way leading to a sub-segmentation. Then a finer segmentation is obtained by computing $\eta$-bounded regions and $\mu$-geodesic balls inside the $\lambda$-flat zones. The proposed algorithms for the construction of new partitions are based on queues with an ordered selection of seeds using the cumulative distance. $\eta$-bounded regions offers a control on the variations of amplitude in the class from a point, called center, and $\mu$-geodesic balls controls the "size" of the class. These results are applied to hyperspectral images.