On distances, paths and connections for hyperspectral image segmentation
Paper and Code
Feb 02, 2016

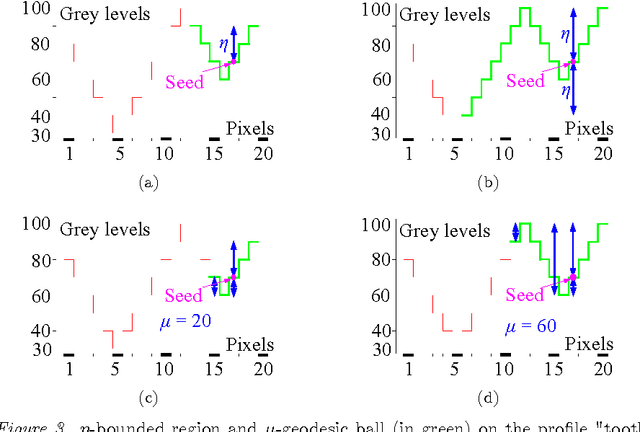

The present paper introduces the $\eta$ and {\eta} connections in order to add regional information on $\lambda$-flat zones, which only take into account a local information. A top-down approach is considered. First $\lambda$-flat zones are built in a way leading to a sub-segmentation. Then a finer segmentation is obtained by computing $\eta$-bounded regions and $\mu$-geodesic balls inside the $\lambda$-flat zones. The proposed algorithms for the construction of new partitions are based on queues with an ordered selection of seeds using the cumulative distance. $\eta$-bounded regions offers a control on the variations of amplitude in the class from a point, called center, and $\mu$-geodesic balls controls the "size" of the class. These results are applied to hyperspectral images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge