Block Graph Neural Networks for tumor heterogeneity prediction

Accurate tumor classification is essential for selecting effective treatments, but current methods have limitations. Standard tumor grading, which categorizes tumors based on cell differentiation, is not recommended as a stand-alone procedure, as some well-differentiated tumors can be malignant. Tumor heterogeneity assessment via single-cell sequencing offers profound insights but can be costly and may still require significant manual intervention. Many existing statistical machine learning methods for tumor data still require complex pre-processing of MRI and histopathological data. In this paper, we propose to build on a mathematical model that simulates tumor evolution (O\.{z}a\'{n}ski (2017)) and generate artificial datasets for tumor classification. Tumor heterogeneity is estimated using normalized entropy, with a threshold to classify tumors as having high or low heterogeneity. Our contributions are threefold: (1) the cut and graph generation processes from the artificial data, (2) the design of tumor features, and (3) the construction of Block Graph Neural Networks (BGNN), a Graph Neural Network-based approach to predict tumor heterogeneity. The experimental results reveal that the combination of the proposed features and models yields excellent results on artificially generated data ($89.67\%$ accuracy on the test data). In particular, in alignment with the emerging trends in AI-assisted grading and spatial transcriptomics, our results suggest that enriching traditional grading methods with birth (e.g., Ki-67 proliferation index) and death markers can improve heterogeneity prediction and enhance tumor classification.

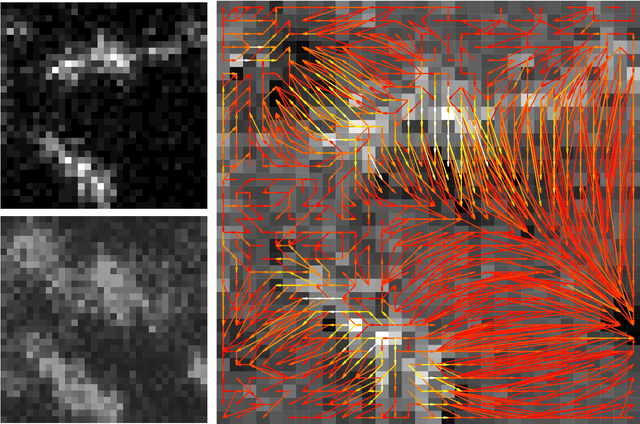
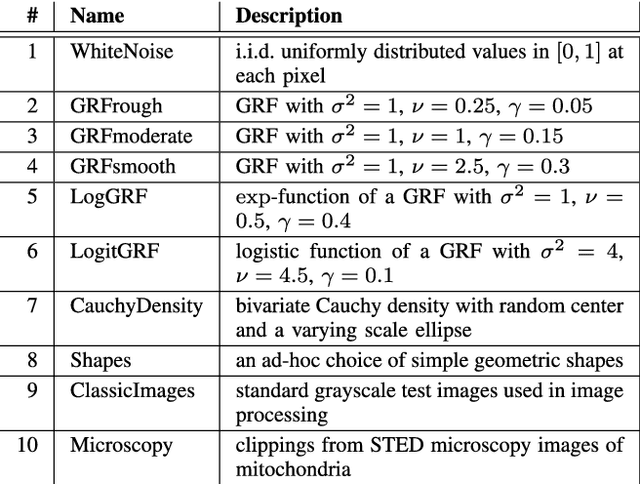
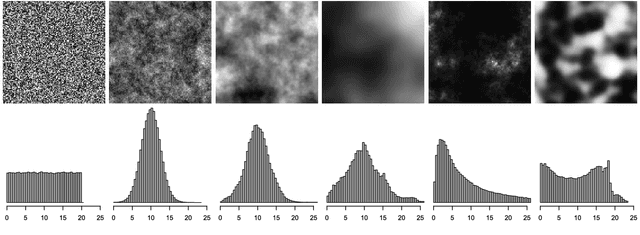
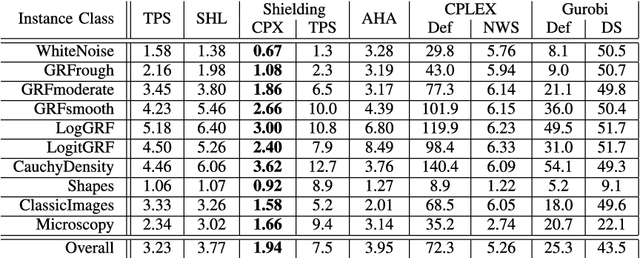
DOTmark - A Benchmark for Discrete Optimal Transport

The Wasserstein metric or earth mover's distance (EMD) is a useful tool in statistics, machine learning and computer science with many applications to biological or medical imaging, among others. Especially in the light of increasingly complex data, the computation of these distances via optimal transport is often the limiting factor. Inspired by this challenge, a variety of new approaches to optimal transport has been proposed in recent years and along with these new methods comes the need for a meaningful comparison. In this paper, we introduce a benchmark for discrete optimal transport, called DOTmark, which is designed to serve as a neutral collection of problems, where discrete optimal transport methods can be tested, compared to one another, and brought to their limits on large-scale instances. It consists of a variety of grayscale images, in various resolutions and classes, such as several types of randomly generated images, classical test images and real data from microscopy. Along with the DOTmark we present a survey and a performance test for a cross section of established methods ranging from more traditional algorithms, such as the transportation simplex, to recently developed approaches, such as the shielding neighborhood method, and including also a comparison with commercial solvers.

The Shortlist Method for Fast Computation of the Earth Mover's Distance and Finding Optimal Solutions to Transportation Problems

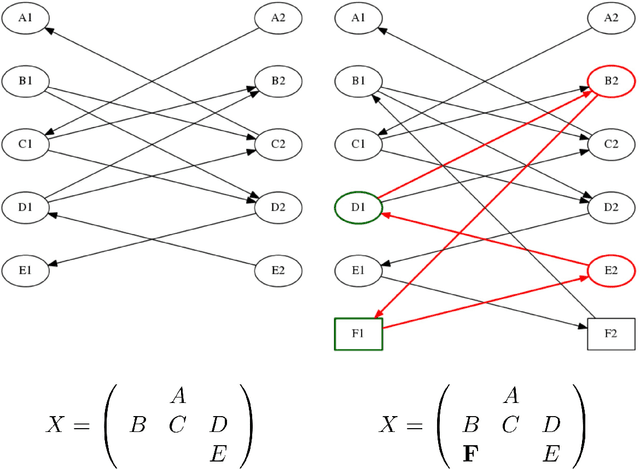
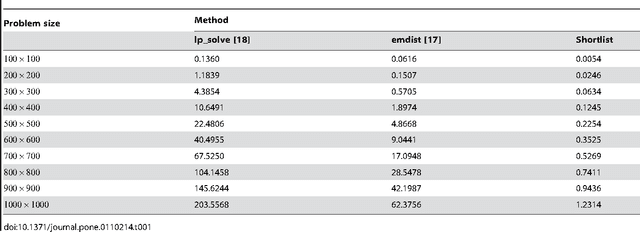
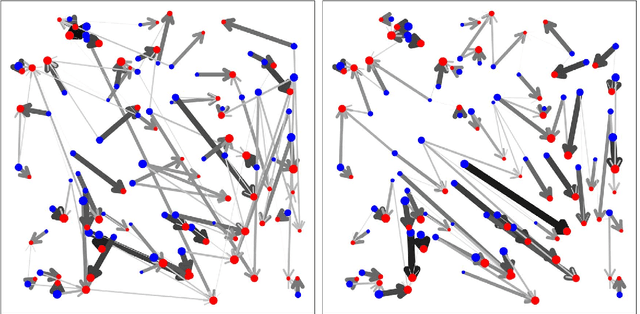
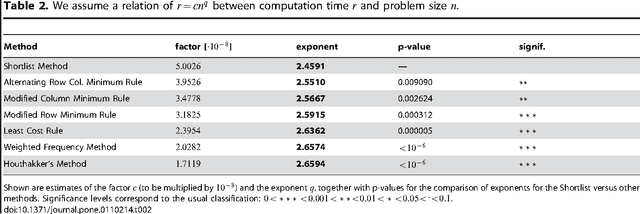
Finding solutions to the classical transportation problem is of great importance, since this optimization problem arises in many engineering and computer science applications. Especially the Earth Mover's Distance is used in a plethora of applications ranging from content-based image retrieval, shape matching, fingerprint recognition, object tracking and phishing web page detection to computing color differences in linguistics and biology. Our starting point is the well-known revised simplex algorithm, which iteratively improves a feasible solution to optimality. The Shortlist Method that we propose substantially reduces the number of candidates inspected for improving the solution, while at the same time balancing the number of pivots required. Tests on simulated benchmarks demonstrate a considerable reduction in computation time for the new method as compared to the usual revised simplex algorithm implemented with state-of-the-art initialization and pivot strategies. As a consequence, the Shortlist Method facilitates the computation of large scale transportation problems in viable time. In addition we describe a novel method for finding an initial feasible solution which we coin Modified Russell's Method.