Barcodes as summary of objective function's topology

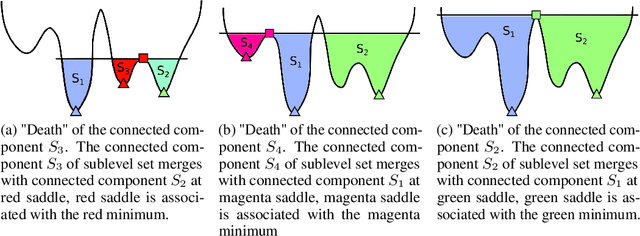
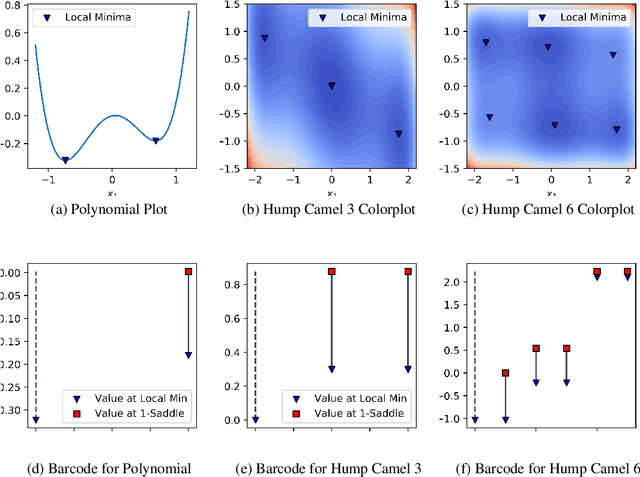
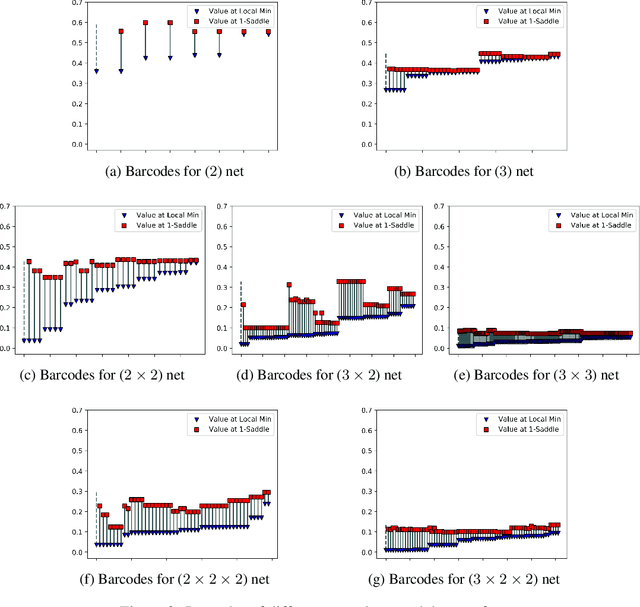
We apply the canonical forms (barcodes) of gradient Morse complexes to explore topology of loss surfaces. We present a new algorithm for calculations of the objective function's barcodes of minima. Our experiments confirm two principal observations: 1) the barcodes of minima are located in a small lower part of the range of values of loss function of neural networks, 2) an increase of the neural network's depth brings down the minima's barcodes. This has natural implications for the neural network's learning and generalization ability.