NeuroGame Transformer: Gibbs-Inspired Attention Driven by Game Theory and Statistical Physics

Standard attention mechanisms in transformers are limited by their pairwise formulation, which hinders the modeling of higher-order dependencies among tokens. We introduce the NeuroGame Transformer (NGT) to overcome this by reconceptualizing attention through a dual perspective: tokens are treated simultaneously as players in a cooperative game and as interacting spins in a statistical physics system. Token importance is quantified using two complementary game-theoretic concepts -- Shapley values for global, permutation-based attribution and Banzhaf indices for local, coalition-level influence. These are combined via a learnable gating parameter to form an external magnetic field, while pairwise interaction potentials capture synergistic relationships. The system's energy follows an Ising Hamiltonian, with attention weights emerging as marginal probabilities under the Gibbs distribution, efficiently computed via mean-field equations. To ensure scalability despite the exponential coalition space, we develop importance-weighted Monte Carlo estimators with Gibbs-distributed weights. This approach avoids explicit exponential factors, ensuring numerical stability for long sequences. We provide theoretical convergence guarantees and characterize the fairness-sensitivity trade-off governed by the interpolation parameter. Experimental results demonstrate that the NeuroGame Transformer achieves strong performance across SNLI, and MNLI-matched, outperforming some major efficient transformer baselines. On SNLI, it attains a test accuracy of 86.4\% (with a peak validation accuracy of 86.6\%), surpassing ALBERT-Base and remaining highly competitive with RoBERTa-Base. Code is available at https://github.com/dbouchaffra/NeuroGame-Transformer.

Game Theory Meets Statistical Mechanics in Deep Learning Design

We present a novel deep graphical representation that seamlessly merges principles of game theory with laws of statistical mechanics. It performs feature extraction, dimensionality reduction, and pattern classification within a single learning framework. Our approach draws an analogy between neurons in a network and players in a game theory model. Furthermore, each neuron viewed as a classical particle (subject to statistical physics' laws) is mapped to a set of actions representing specific activation value, and neural network layers are conceptualized as games in a sequential cooperative game theory setting. The feed-forward process in deep learning is interpreted as a sequential game, where each game comprises a set of players. During training, neurons are iteratively evaluated and filtered based on their contributions to a payoff function, which is quantified using the Shapley value driven by an energy function. Each set of neurons that significantly contributes to the payoff function forms a strong coalition. These neurons are the only ones permitted to propagate the information forward to the next layers. We applied this methodology to the task of facial age estimation and gender classification. Experimental results demonstrate that our approach outperforms both multi-layer perceptron and convolutional neural network models in terms of efficiency and accuracy.

Adaptative Context Normalization: A Boost for Deep Learning in Image Processing

Deep Neural network learning for image processing faces major challenges related to changes in distribution across layers, which disrupt model convergence and performance. Activation normalization methods, such as Batch Normalization (BN), have revolutionized this field, but they rely on the simplified assumption that data distribution can be modelled by a single Gaussian distribution. To overcome these limitations, Mixture Normalization (MN) introduced an approach based on a Gaussian Mixture Model (GMM), assuming multiple components to model the data. However, this method entails substantial computational requirements associated with the use of Expectation-Maximization algorithm to estimate parameters of each Gaussian components. To address this issue, we introduce Adaptative Context Normalization (ACN), a novel supervised approach that introduces the concept of "context", which groups together a set of data with similar characteristics. Data belonging to the same context are normalized using the same parameters, enabling local representation based on contexts. For each context, the normalized parameters, as the model weights are learned during the backpropagation phase. ACN not only ensures speed, convergence, and superior performance compared to BN and MN but also presents a fresh perspective that underscores its particular efficacy in the field of image processing.

Context-Based Multimodal Fusion

The fusion models, which effectively combine information from different sources, are widely used in solving multimodal tasks. However, they have significant limitations related to aligning data distributions across different modalities. This challenge can lead to inconsistencies and difficulties in learning robust representations. Alignment models, while specifically addressing this issue, often require training "from scratch" with large datasets to achieve optimal results, which can be costly in terms of resources and time. To overcome these limitations, we propose an innovative model called Context-Based Multimodal Fusion (CBMF), which combines both modality fusion and data distribution alignment. In CBMF, each modality is represented by a specific context vector, fused with the embedding of each modality. This enables the use of large pre-trained models that can be frozen, reducing the computational and training data requirements. Additionally, the network learns to differentiate embeddings of different modalities through fusion with context and aligns data distributions using a contrastive approach for self-supervised learning. Thus, CBMF offers an effective and economical solution for solving complex multimodal tasks.

Distributed Collapsed Gibbs Sampler for Dirichlet Process Mixture Models in Federated Learning

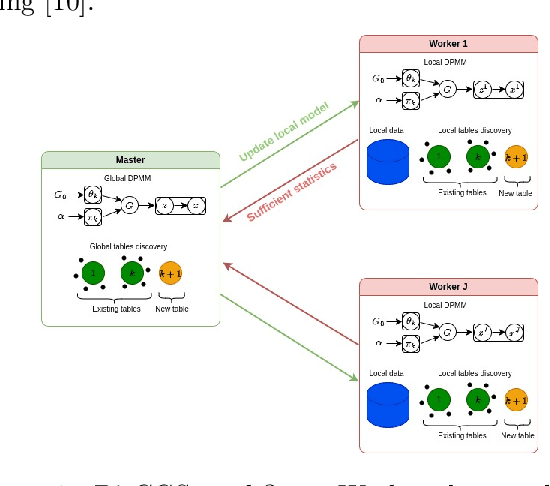
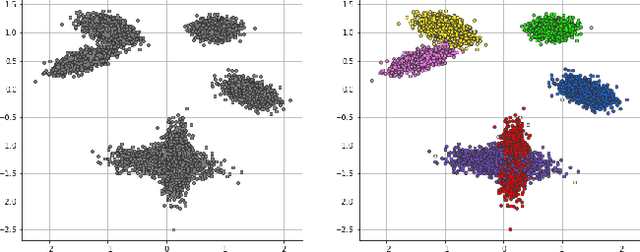
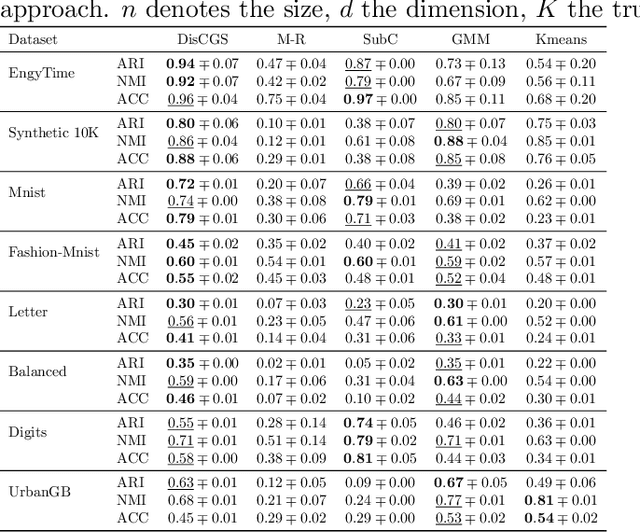
Dirichlet Process Mixture Models (DPMMs) are widely used to address clustering problems. Their main advantage lies in their ability to automatically estimate the number of clusters during the inference process through the Bayesian non-parametric framework. However, the inference becomes considerably slow as the dataset size increases. This paper proposes a new distributed Markov Chain Monte Carlo (MCMC) inference method for DPMMs (DisCGS) using sufficient statistics. Our approach uses the collapsed Gibbs sampler and is specifically designed to work on distributed data across independent and heterogeneous machines, which habilitates its use in horizontal federated learning. Our method achieves highly promising results and notable scalability. For instance, with a dataset of 100K data points, the centralized algorithm requires approximately 12 hours to complete 100 iterations while our approach achieves the same number of iterations in just 3 minutes, reducing the execution time by a factor of 200 without compromising clustering performance. The code source is publicly available at https://github.com/redakhoufache/DisCGS.