Dingsheng Wan
Applications of Social Media in Hydroinformatics: A Survey
May 01, 2019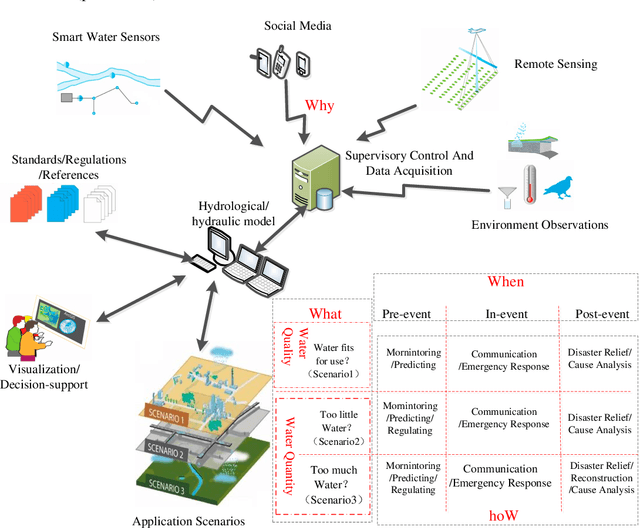
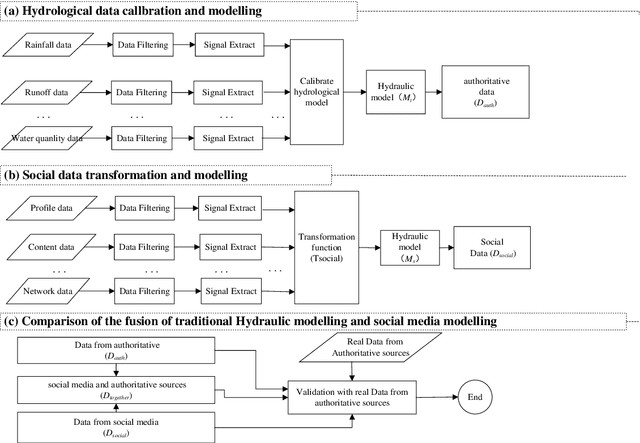
Abstract:Floods of research and practical applications employ social media data for a wide range of public applications, including environmental monitoring, water resource managing, disaster and emergency response.Hydroinformatics can benefit from the social media technologies with newly emerged data, techniques and analytical tools to handle large datasets, from which creative ideas and new values could be mined.This paper first proposes a 4W (What, Why, When, hoW) model and a methodological structure to better understand and represent the application of social media to hydroinformatics, then provides an overview of academic research of applying social media to hydroinformatics such as water environment, water resources, flood, drought and water Scarcity management. At last,some advanced topics and suggestions of water related social media applications from data collection, data quality management, fake news detection, privacy issues, algorithms and platforms was present to hydroinformatics managers and researchers based on previous discussion.
A Novel Trend Symbolic Aggregate Approximation for Time Series
May 01, 2019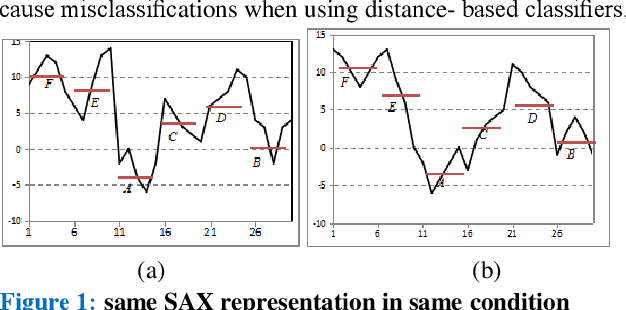
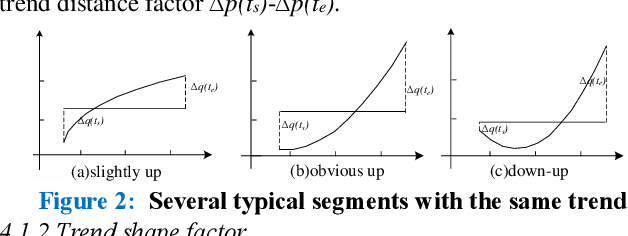
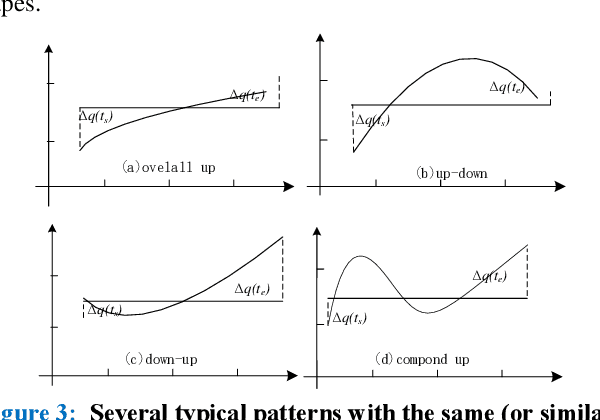
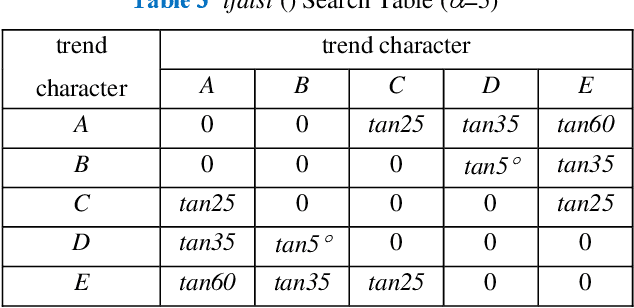
Abstract:Symbolic Aggregate approximation (SAX) is a classical symbolic approach in many time series data mining applications. However, SAX only reflects the segment mean value feature and misses important information in a segment, namely the trend of the value change in the segment. Such a miss may cause a wrong classification in some cases, since the SAX representation cannot distinguish different time series with similar average values but different trends. In this paper, we present Trend Feature Symbolic Aggregate approximation (TFSAX) to solve this problem. First, we utilize Piecewise Aggregate Approximation (PAA) approach to reduce dimensionality and discretize the mean value of each segment by SAX. Second, extract trend feature in each segment by using trend distance factor and trend shape factor. Then, design multi-resolution symbolic mapping rules to discretize trend information into symbols. We also propose a modified distance measure by integrating the SAX distance with a weighted trend distance. We show that our distance measure has a tighter lower bound to the Euclidean distance than that of the original SAX. The experimental results on diverse time series data sets demonstrate that our proposed representation significantly outperforms the original SAX representation and an improved SAX representation for classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge