Dimitris Floros
Spaceland Embedding of Sparse Stochastic Graphs
Jun 13, 2019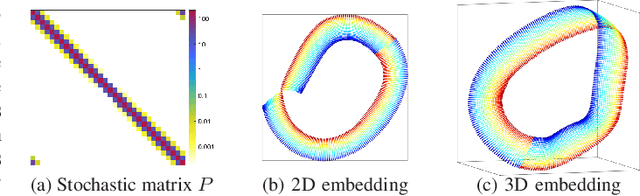


Abstract:We introduce a nonlinear method for directly embedding large, sparse, stochastic graphs into low-dimensional spaces, without requiring vertex features to reside in, or be transformed into, a metric space. Graph data and models are prevalent in real-world applications. Direct graph embedding is fundamental to many graph analysis tasks, in addition to graph visualization. We name the novel approach SG-t-SNE, as it is inspired by and builds upon the core principle of t-SNE, a widely used method for nonlinear dimensionality reduction and data visualization. We also introduce t-SNE-$\Pi$, a high-performance software for 2D, 3D embedding of large sparse graphs on personal computers with superior efficiency. It empowers SG-t-SNE with modern computing techniques for exploiting in tandem both matrix structures and memory architectures. We present elucidating embedding results on one synthetic graph and four real-world networks.
Rapid Near-Neighbor Interaction of High-dimensional Data via Hierarchical Clustering
Sep 12, 2017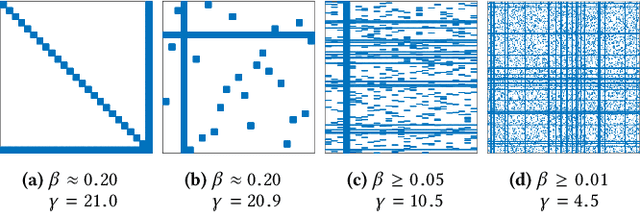
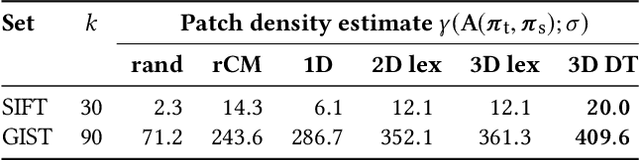
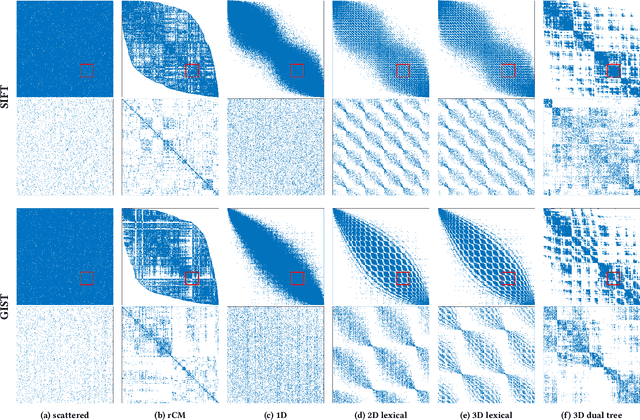
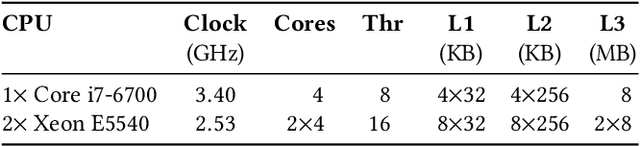
Abstract:Calculation of near-neighbor interactions among high dimensional, irregularly distributed data points is a fundamental task to many graph-based or kernel-based machine learning algorithms and applications. Such calculations, involving large, sparse interaction matrices, expose the limitation of conventional data-and-computation reordering techniques for improving space and time locality on modern computer memory hierarchies. We introduce a novel method for obtaining a matrix permutation that renders a desirable sparsity profile. The method is distinguished by the guiding principle to obtain a profile that is block-sparse with dense blocks. Our profile model and measure capture the essential properties affecting space and time locality, and permit variation in sparsity profile without imposing a restriction to a fixed pattern. The second distinction lies in an efficient algorithm for obtaining a desirable profile, via exploring and exploiting multi-scale cluster structure hidden in but intrinsic to the data. The algorithm accomplishes its task with key components for lower-dimensional embedding with data-specific principal feature axes, hierarchical data clustering, multi-level matrix compression storage, and multi-level interaction computations. We provide experimental results from case studies with two important data analysis algorithms. The resulting performance is remarkably comparable to the BLAS performance for the best-case interaction governed by a regularly banded matrix with the same sparsity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge