Spaceland Embedding of Sparse Stochastic Graphs
Paper and Code
Jun 13, 2019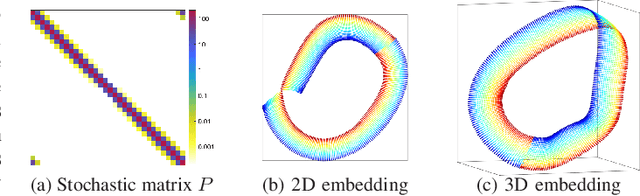
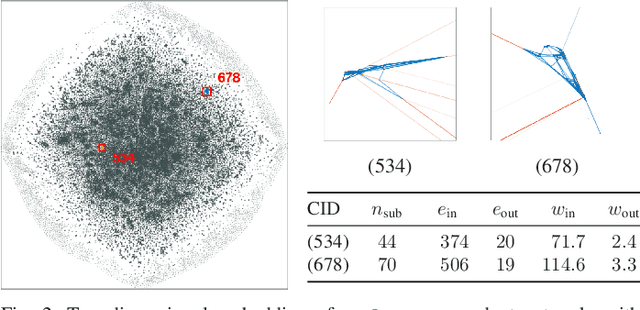


We introduce a nonlinear method for directly embedding large, sparse, stochastic graphs into low-dimensional spaces, without requiring vertex features to reside in, or be transformed into, a metric space. Graph data and models are prevalent in real-world applications. Direct graph embedding is fundamental to many graph analysis tasks, in addition to graph visualization. We name the novel approach SG-t-SNE, as it is inspired by and builds upon the core principle of t-SNE, a widely used method for nonlinear dimensionality reduction and data visualization. We also introduce t-SNE-$\Pi$, a high-performance software for 2D, 3D embedding of large sparse graphs on personal computers with superior efficiency. It empowers SG-t-SNE with modern computing techniques for exploiting in tandem both matrix structures and memory architectures. We present elucidating embedding results on one synthetic graph and four real-world networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge