An Optimization-based Deep Equilibrium Model for Hyperspectral Image Deconvolution with Convergence Guarantees

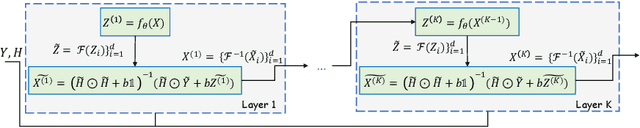
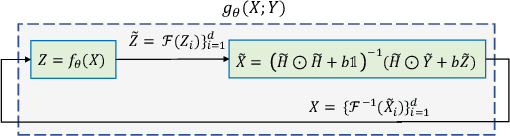
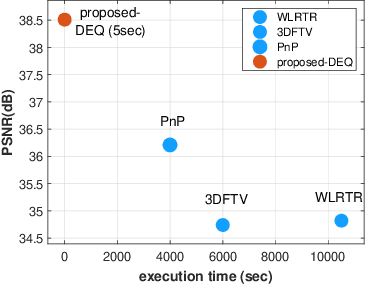
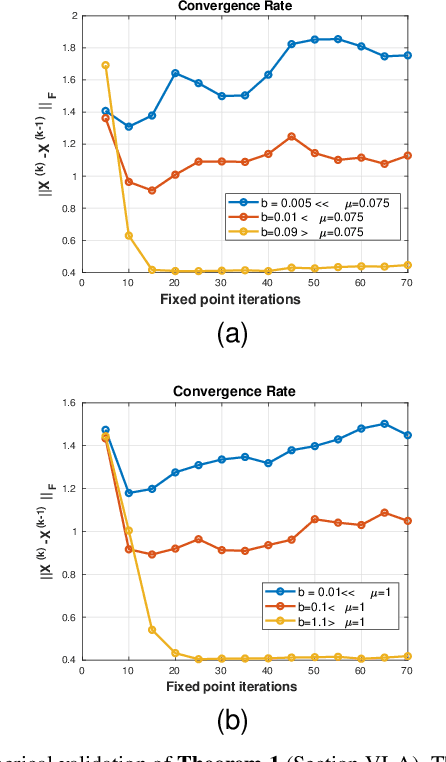
In this paper, we propose a novel methodology for addressing the hyperspectral image deconvolution problem. This problem is highly ill-posed, and thus, requires proper priors (regularizers) to model the inherent spectral-spatial correlations of the HSI signals. To this end, a new optimization problem is formulated, leveraging a learnable regularizer in the form of a neural network. To tackle this problem, an effective solver is proposed using the half quadratic splitting methodology. The derived iterative solver is then expressed as a fixed-point calculation problem within the Deep Equilibrium (DEQ) framework, resulting in an interpretable architecture, with clear explainability to its parameters and convergence properties with practical benefits. The proposed model is a first attempt to handle the classical HSI degradation problem with different blurring kernels and noise levels via a single deep equilibrium model with significant computational efficiency. Extensive numerical experiments validate the superiority of the proposed methodology over other state-of-the-art methods. This superior restoration performance is achieved while requiring 99.85\% less computation time as compared to existing methods.

Deep Equilibrium Models Meet Federated Learning

In this study the problem of Federated Learning (FL) is explored under a new perspective by utilizing the Deep Equilibrium (DEQ) models instead of conventional deep learning networks. We claim that incorporating DEQ models into the federated learning framework naturally addresses several open problems in FL, such as the communication overhead due to the sharing large models and the ability to incorporate heterogeneous edge devices with significantly different computation capabilities. Additionally, a weighted average fusion rule is proposed at the server-side of the FL framework to account for the different qualities of models from heterogeneous edge devices. To the best of our knowledge, this study is the first to establish a connection between DEQ models and federated learning, contributing to the development of an efficient and effective FL framework. Finally, promising initial experimental results are presented, demonstrating the potential of this approach in addressing challenges of FL.

Deep Equilibrium Assisted Block Sparse Coding of Inter-dependent Signals: Application to Hyperspectral Imaging

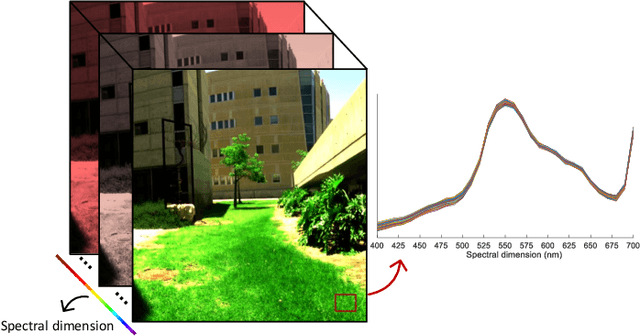
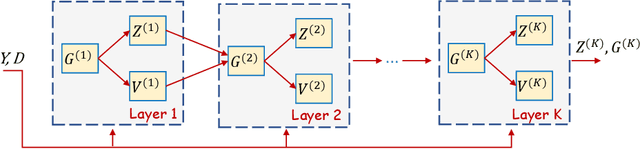
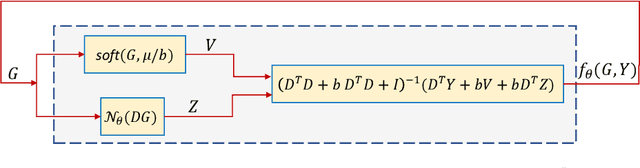
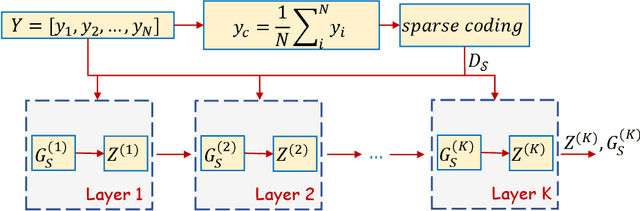
In this study, the problem of computing a sparse representation for datasets of inter-dependent signals, given a fixed dictionary, is considered. A dataset of inter-dependent signals is defined as a matrix whose columns demonstrate strong dependencies. A computational efficient sparse coding optimization problem is derived by employing regularization terms that are adapted to the properties of the signals of interest. Exploiting the merits of the learnable regularization techniques, a neural network is employed to act as structure prior and reveal the underlying signal interdependencies. To solve the optimization problem Deep unrolling and Deep equilibrium based algorithms are developed, forming highly interpretable and concise deep-learning-based architectures, that process the input dataset in a block-by-block fashion. Extensive simulation results, in the context of hyperspectral image denoising, are provided, that demonstrate that the proposed algorithms outperform significantly other sparse coding approaches and exhibit superior performance against recent state-of-the-art deep-learning-based denoising models. In a wider perspective, our work provides a unique bridge between a classic approach, that is the sparse representation theory, and modern representation tools that are based on deep learning modeling.