Deep Equilibrium Assisted Block Sparse Coding of Inter-dependent Signals: Application to Hyperspectral Imaging

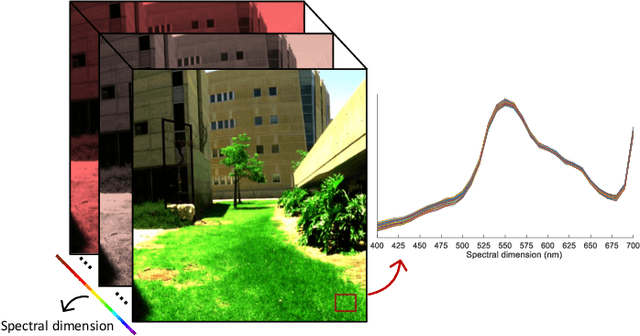
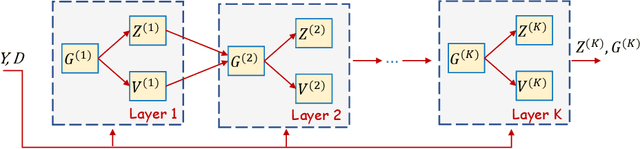
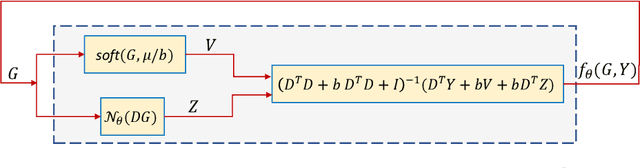
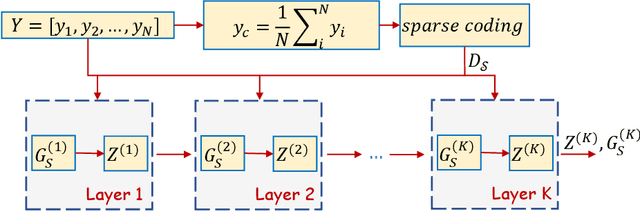
In this study, the problem of computing a sparse representation for datasets of inter-dependent signals, given a fixed dictionary, is considered. A dataset of inter-dependent signals is defined as a matrix whose columns demonstrate strong dependencies. A computational efficient sparse coding optimization problem is derived by employing regularization terms that are adapted to the properties of the signals of interest. Exploiting the merits of the learnable regularization techniques, a neural network is employed to act as structure prior and reveal the underlying signal interdependencies. To solve the optimization problem Deep unrolling and Deep equilibrium based algorithms are developed, forming highly interpretable and concise deep-learning-based architectures, that process the input dataset in a block-by-block fashion. Extensive simulation results, in the context of hyperspectral image denoising, are provided, that demonstrate that the proposed algorithms outperform significantly other sparse coding approaches and exhibit superior performance against recent state-of-the-art deep-learning-based denoising models. In a wider perspective, our work provides a unique bridge between a classic approach, that is the sparse representation theory, and modern representation tools that are based on deep learning modeling.