Enhancing Fairness in Neural Networks Using FairVIC

Mitigating bias in automated decision-making systems, specifically deep learning models, is a critical challenge in achieving fairness. This complexity stems from factors such as nuanced definitions of fairness, unique biases in each dataset, and the trade-off between fairness and model accuracy. To address such issues, we introduce FairVIC, an innovative approach designed to enhance fairness in neural networks by addressing inherent biases at the training stage. FairVIC differs from traditional approaches that typically address biases at the data preprocessing stage. Instead, it integrates variance, invariance and covariance into the loss function to minimise the model's dependency on protected characteristics for making predictions, thus promoting fairness. Our experimentation and evaluation consists of training neural networks on three datasets known for their biases, comparing our results to state-of-the-art algorithms, evaluating on different sizes of model architectures, and carrying out sensitivity analysis to examine the fairness-accuracy trade-off. Through our implementation of FairVIC, we observed a significant improvement in fairness across all metrics tested, without compromising the model's accuracy to a detrimental extent. Our findings suggest that FairVIC presents a straightforward, out-of-the-box solution for the development of fairer deep learning models, thereby offering a generalisable solution applicable across many tasks and datasets.

ChatGPT as a Text Simplification Tool to Remove Bias

The presence of specific linguistic signals particular to a certain sub-group of people can be picked up by language models during training. This may lead to discrimination if the model has learnt to pick up on a certain group's language. If the model begins to associate specific language with a distinct group, any decisions made based upon this language would hold a strong correlation to a decision based on their protected characteristic. We explore a possible technique for bias mitigation in the form of simplification of text. The driving force of this idea is that simplifying text should standardise language to one way of speaking while keeping the same meaning. The experiment shows promising results as the classifier accuracy for predicting the sensitive attribute drops by up to 17% for the simplified data.

Unified Framework for the Adaptive Operator Selection of Discrete Parameters

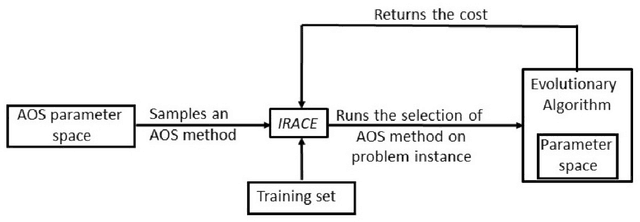
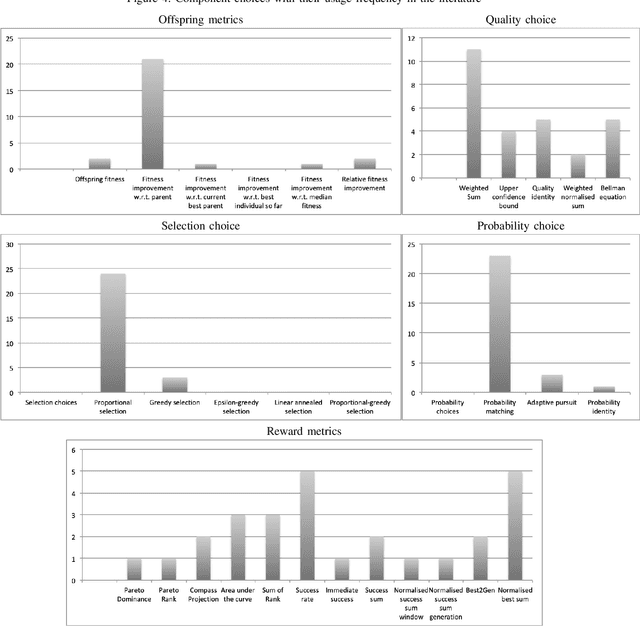
We conduct an exhaustive survey of adaptive selection of operators (AOS) in Evolutionary Algorithms (EAs). We simplified the AOS structure by adding more components to the framework to built upon the existing categorisation of AOS methods. In addition to simplifying, we looked at the commonality among AOS methods from literature to generalise them. Each component is presented with a number of alternative choices, each represented with a formula. We make three sets of comparisons. First, the methods from literature are tested on the BBOB test bed with their default hyper parameters. Second, the hyper parameters of these methods are tuned using an offline configurator known as IRACE. Third, for a given set of problems, we use IRACE to select the best combination of components and tune their hyper parameters.

Deep Reinforcement Learning Based Parameter Control in Differential Evolution

Adaptive Operator Selection (AOS) is an approach that controls discrete parameters of an Evolutionary Algorithm (EA) during the run. In this paper, we propose an AOS method based on Double Deep Q-Learning (DDQN), a Deep Reinforcement Learning method, to control the mutation strategies of Differential Evolution (DE). The application of DDQN to DE requires two phases. First, a neural network is trained offline by collecting data about the DE state and the benefit (reward) of applying each mutation strategy during multiple runs of DE tackling benchmark functions. We define the DE state as the combination of 99 different features and we analyze three alternative reward functions. Second, when DDQN is applied as a parameter controller within DE to a different test set of benchmark functions, DDQN uses the trained neural network to predict which mutation strategy should be applied to each parent at each generation according to the DE state. Benchmark functions for training and testing are taken from the CEC2005 benchmark with dimensions 10 and 30. We compare the results of the proposed DE-DDQN algorithm to several baseline DE algorithms using no online selection, random selection and other AOS methods, and also to the two winners of the CEC2005 competition. The results show that DE-DDQN outperforms the non-adaptive methods for all functions in the test set; while its results are comparable with the last two algorithms.

Creating a level playing field for all symbols in a discretization

In time series analysis research there is a strong interest in discrete representations of real valued data streams. One approach that emerged over a decade ago and is still considered state-of-the-art is the Symbolic Aggregate Approximation algorithm. This discretization algorithm was the first symbolic approach that mapped a real-valued time series to a symbolic representation that was guaranteed to lower-bound Euclidean distance. The interest of this paper concerns the SAX assumption of data being highly Gaussian and the use of the standard normal curve to choose partitions to discretize the data. Though not necessarily, but generally, and certainly in its canonical form, the SAX approach chooses partitions on the standard normal curve that would produce an equal probability for each symbol in a finite alphabet to occur. This procedure is generally valid as a time series is normalized before the rest of the SAX algorithm is applied. However there exists a caveat to this assumption of equi-probability due to the intermediate step of Piecewise Aggregate Approximation (PAA). What we will show in this paper is that when PAA is applied the distribution of the data is indeed altered, resulting in a shrinking standard deviation that is proportional to the number of points used to create a segment of the PAA representation and the degree of auto-correlation within the series. Data that exhibits statistically significant auto-correlation is less affected by this shrinking distribution. As the standard deviation of the data contracts, the mean remains the same, however the distribution is no longer standard normal and therefore the partitions based on the standard normal curve are no longer valid for the assumption of equal probability.