Diego Pérez-López
Incorporating Recklessness to Collaborative Filtering based Recommender Systems
Aug 03, 2023
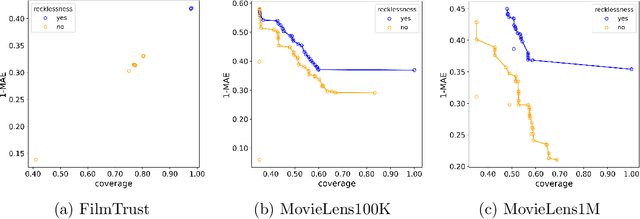
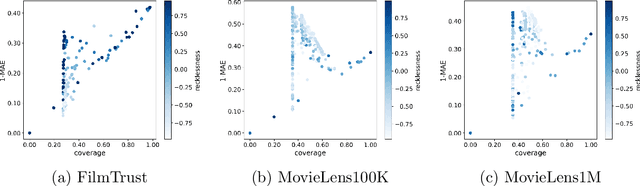
Abstract:Recommender systems that include some reliability measure of their predictions tend to be more conservative in forecasting, due to their constraint to preserve reliability. This leads to a significant drop in the coverage and novelty that these systems can provide. In this paper, we propose the inclusion of a new term in the learning process of matrix factorization-based recommender systems, called recklessness, which enables the control of the risk level desired when making decisions about the reliability of a prediction. Experimental results demonstrate that recklessness not only allows for risk regulation but also improves the quantity and quality of predictions provided by the recommender system.
An evaluation framework for dimensionality reduction through sectional curvature
Mar 17, 2023Abstract:Unsupervised machine learning lacks ground truth by definition. This poses a major difficulty when designing metrics to evaluate the performance of such algorithms. In sharp contrast with supervised learning, for which plenty of quality metrics have been studied in the literature, in the field of dimensionality reduction only a few over-simplistic metrics has been proposed. In this work, we aim to introduce the first highly non-trivial dimensionality reduction performance metric. This metric is based on the sectional curvature behaviour arising from Riemannian geometry. To test its feasibility, this metric has been used to evaluate the performance of the most commonly used dimension reduction algorithms in the state of the art. Furthermore, to make the evaluation of the algorithms robust and representative, using curvature properties of planar curves, a new parameterized problem instance generator has been constructed in the form of a function generator. Experimental results are consistent with what could be expected based on the design and characteristics of the evaluated algorithms and the features of the data instances used to feed the method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge