Inversion using a new low-dimensional representation of complex binary geological media based on a deep neural network

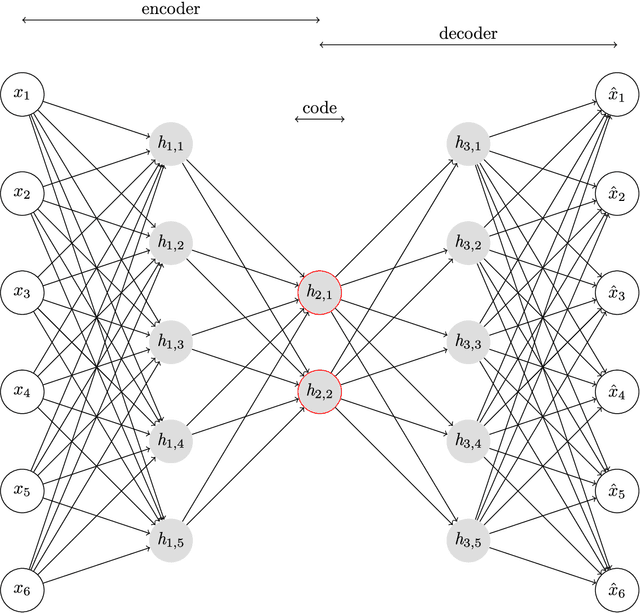
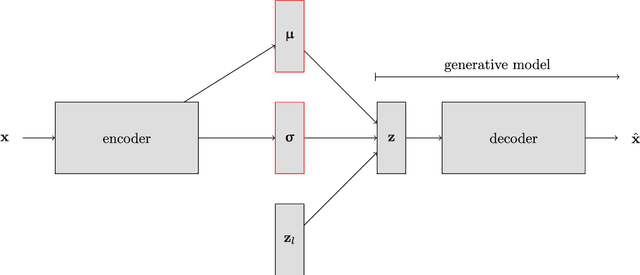
Efficient and high-fidelity prior sampling and inversion for complex geological media is still a largely unsolved challenge. Here, we use a deep neural network of the variational autoencoder type to construct a parametric low-dimensional base model parameterization of complex binary geological media. For inversion purposes, it has the attractive feature that random draws from an uncorrelated standard normal distribution yield model realizations with spatial characteristics that are in agreement with the training set. In comparison with the most commonly used parametric representations in probabilistic inversion, we find that our dimensionality reduction (DR) approach outperforms principle component analysis (PCA), optimization-PCA (OPCA) and discrete cosine transform (DCT) DR techniques for unconditional geostatistical simulation of a channelized prior model. For the considered examples, important compression ratios (200 - 500) are achieved. Given that the construction of our parameterization requires a training set of several tens of thousands of prior model realizations, our DR approach is more suited for probabilistic (or deterministic) inversion than for unconditional (or point-conditioned) geostatistical simulation. Probabilistic inversions of 2D steady-state and 3D transient hydraulic tomography data are used to demonstrate the DR-based inversion. For the 2D case study, the performance is superior compared to current state-of-the-art multiple-point statistics inversion by sequential geostatistical resampling (SGR). Inversion results for the 3D application are also encouraging.

Efficient training-image based geostatistical simulation and inversion using a spatial generative adversarial neural network

Probabilistic inversion within a multiple-point statistics framework is still computationally prohibitive for large-scale problems. To partly address this, we introduce and evaluate a new training-image based simulation and inversion approach for complex geologic media. Our approach relies on a deep neural network of the spatial generative adversarial network (SGAN) type. After training using a training image (TI), our proposed SGAN can quickly generate 2D and 3D unconditional realizations. A key feature of our SGAN is that it defines a (very) low-dimensional parameterization, thereby allowing for efficient probabilistic (or deterministic) inversion using state-of-the-art Markov chain Monte Carlo (MCMC) methods. A series of 2D and 3D categorical TIs is first used to analyze the performance of our SGAN for unconditional simulation. The speed at which realizations are generated makes it especially useful for simulating over large grids and/or from a complex multi-categorical TI. Subsequently, synthetic inversion case studies involving 2D steady-state flow and 3D transient hydraulic tomography are used to illustrate the effectiveness of our proposed SGAN-based probabilistic inversion. For the 2D case, the inversion rapidly explores the posterior model distribution. For the 3D case, the inversion recovers model realizations that fit the data close to the target level and visually resemble the true model well. Future work will focus on the inclusion of direct conditioning data and application to continuous TIs.