Inversion using a new low-dimensional representation of complex binary geological media based on a deep neural network
Paper and Code
Oct 25, 2017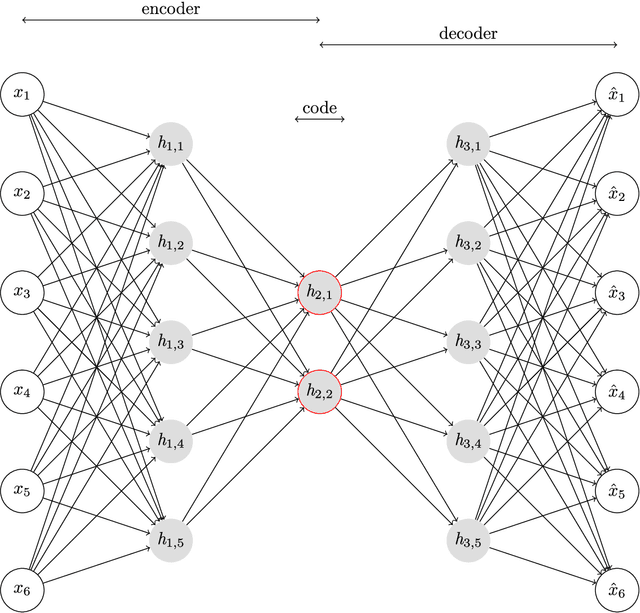
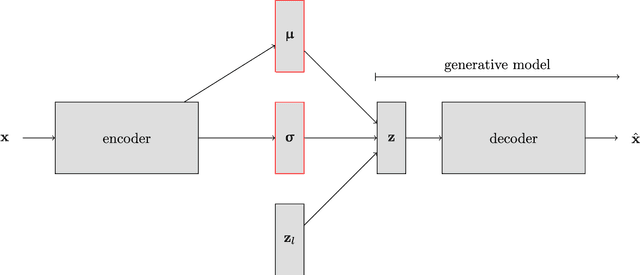

Efficient and high-fidelity prior sampling and inversion for complex geological media is still a largely unsolved challenge. Here, we use a deep neural network of the variational autoencoder type to construct a parametric low-dimensional base model parameterization of complex binary geological media. For inversion purposes, it has the attractive feature that random draws from an uncorrelated standard normal distribution yield model realizations with spatial characteristics that are in agreement with the training set. In comparison with the most commonly used parametric representations in probabilistic inversion, we find that our dimensionality reduction (DR) approach outperforms principle component analysis (PCA), optimization-PCA (OPCA) and discrete cosine transform (DCT) DR techniques for unconditional geostatistical simulation of a channelized prior model. For the considered examples, important compression ratios (200 - 500) are achieved. Given that the construction of our parameterization requires a training set of several tens of thousands of prior model realizations, our DR approach is more suited for probabilistic (or deterministic) inversion than for unconditional (or point-conditioned) geostatistical simulation. Probabilistic inversions of 2D steady-state and 3D transient hydraulic tomography data are used to demonstrate the DR-based inversion. For the 2D case study, the performance is superior compared to current state-of-the-art multiple-point statistics inversion by sequential geostatistical resampling (SGR). Inversion results for the 3D application are also encouraging.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge