Illumination Robust Loop Closure Detection with the Constraint of Pose

Background: Loop closure detection is a crucial part in robot navigation and simultaneous location and mapping (SLAM). Appearance-based loop closure detection still faces many challenges, such as illumination changes, perceptual aliasing and increasing computational complexity. Method: In this paper, we proposed a visual loop-closure detection algorithm which combines illumination robust descriptor DIRD and odometry information. The estimated pose and variance are calculated by the visual inertial odometry (VIO), then the loop closure candidate areas are found based on the distance between images. We use a new distance combing the the Euclidean distance and the Mahalanobis distance and a dynamic threshold to select the loop closure candidate areas. Finally, in loop-closure candidate areas, we do image retrieval with DIRD which is an illumination robust descriptor. Results: The proposed algorithm is evaluated on KITTI_00 and EuRoc datasets. The results show that the loop closure areas could be correctly detected and the time consumption is effectively reduced. We compare it with SeqSLAM algorithm, the proposed algorithm gets better performance on PR-curve.

Invariant Cubature Kalman Filter for Monocular Visual Inertial Odometry with Line Features

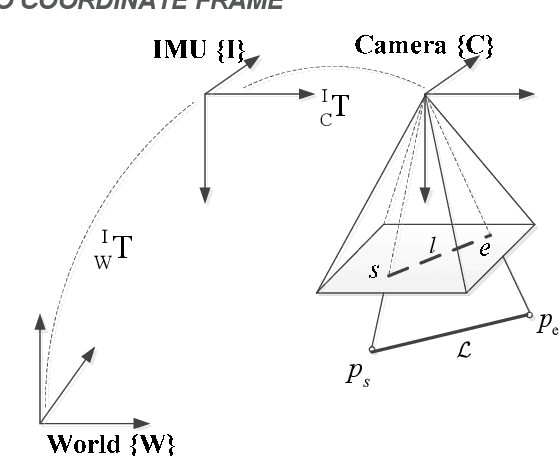
To achieve robust and accurate state estimation for robot navigation, we propose a novel Visual Inertial Odometry(VIO) algorithm with line features upon the theory of invariant Kalman filtering and Cubature Kalman Filter (CKF). In contrast with conventional CKF, the state of the filter is constructed by a high dimensional Matrix Lie group and the uncertainty is represented using Lie algebra. To improve the robustness of system in challenging scenes, e.g. low-texture or illumination changing environments, line features are brought into the state variable. In the proposed algorithm, exponential mapping of Lie algebra is used to construct the cubature points and the re-projection errors of lines are built as observation function for updating the state. This method accurately describes the system uncertainty in rotation and reduces the linearization error of system, which extends traditional CKF from Euclidean space to manifold. It not only inherits the advantages of invariant filtering in consistency, but also avoids the complex Jacobian calculation of high-dimensional matrix. To demonstrate the effectiveness of the proposed algorithm, we compare it with the state-of-the-art filtering-based VIO algorithms on Euroc datasets. And the results show that the proposed algorithm is effective in improving accuracy and robustness of estimation.