Invariant Cubature Kalman Filter for Monocular Visual Inertial Odometry with Line Features
Paper and Code
Dec 26, 2019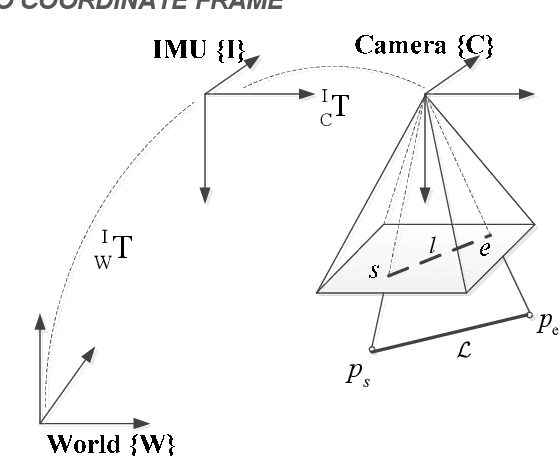



To achieve robust and accurate state estimation for robot navigation, we propose a novel Visual Inertial Odometry(VIO) algorithm with line features upon the theory of invariant Kalman filtering and Cubature Kalman Filter (CKF). In contrast with conventional CKF, the state of the filter is constructed by a high dimensional Matrix Lie group and the uncertainty is represented using Lie algebra. To improve the robustness of system in challenging scenes, e.g. low-texture or illumination changing environments, line features are brought into the state variable. In the proposed algorithm, exponential mapping of Lie algebra is used to construct the cubature points and the re-projection errors of lines are built as observation function for updating the state. This method accurately describes the system uncertainty in rotation and reduces the linearization error of system, which extends traditional CKF from Euclidean space to manifold. It not only inherits the advantages of invariant filtering in consistency, but also avoids the complex Jacobian calculation of high-dimensional matrix. To demonstrate the effectiveness of the proposed algorithm, we compare it with the state-of-the-art filtering-based VIO algorithms on Euroc datasets. And the results show that the proposed algorithm is effective in improving accuracy and robustness of estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge