Lattice All-Pass Filter based Precoder Adaptation for MIMO Wireless Channels

Modern 5G communication systems employ multiple-input multiple-output (MIMO) in conjunction with orthogonal frequency division multiplexing (OFDM) to enhance data rates, particularly for wideband millimetre wave (mmW) applications. Since these systems use a large number of subcarriers, feeding back the estimated precoder for even a subset of subcarriers from the receiver to the transmitter is prohibitive. Moreover, such frequency domain approaches also do not exploit the predominant line-of-sight component that is present in such channels to reduce feedback. In this work, we view the precoder in the time domain as a matrix all-pass filter, and model the discrete-time precoder filter using a matrix-lattice structure that aids in reducing the overall feedback while still maintaining the desired frequency-phase delay profile. This provides an efficient precoder representation across the subcarriers using fewer coefficients, and is amenable to tracking over time with much lower feedback than past approaches. Compared to frequency domain geodesic interpolation, Givens rotation based parameterisation, and the angle-delay domain approach that depends on approximate discrete-time representation, the proposed approach yields higher achievable rates with a much lower feedback burden. Via extensive simulations over mmW channel models, we confirm the effectiveness of our claims, and show that the proposed approach can reduce the feedback burden by up to 70%.

Design of Discrete-time Matrix All-Pass Filters Using Subspace Nevanlinna Pick Interpolation

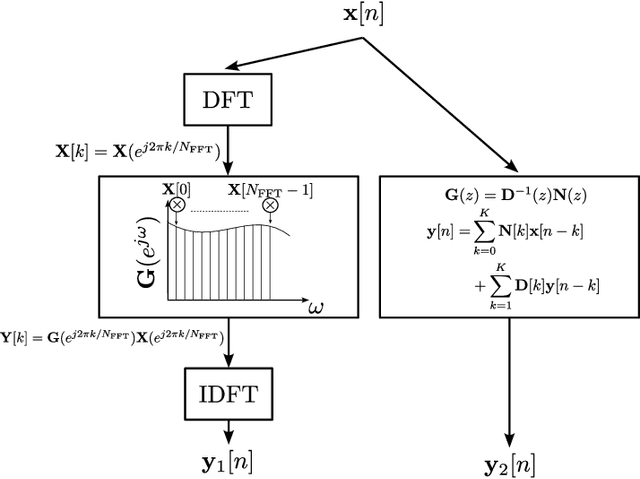
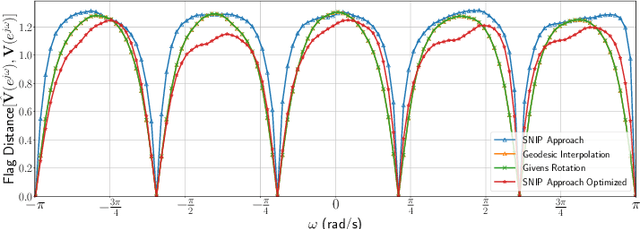
Unitary matrix-valued functions of frequency are matrix all-pass systems, since they preserve the norm of the input vector signals. Typically, such systems are represented and analyzed using their unitary-matrix valued frequency domain characteristics, although obtaining rational realizations for matrix all-pass systems enables compact representations and efficient implementations. However, an approach to obtain matrix all-pass filters that satisfy phase constraints at certain frequencies was hitherto unknown. In this paper, we present an interpolation strategy to obtain a rational matrix-valued transfer function from frequency domain constraints for discrete-time matrix all-pass systems. Using an extension of the Subspace Nevanlinna Pick Interpolation Problem (SNIP), we design a construction for discrete-time matrix all-pass systems that satisfy the desired phase characteristics. An innovation that enables this is the extension of the SNIP to the boundary case to obtain efficient time-domain implementations of matrix all-pass filters as matrix linear constant coefficient difference equations, facilitated by a rational (realizable) matrix transfer function. We also show that the derivative of matrix phase constraints, related to the group delay at the interpolating points, can be optimized to control the all-pass transfer matrices at the unspecified frequencies. Simulations show that the proposed technique for unitary matrix filter design performs as well as traditional DFT based interpolation approaches, including Geodesic interpolation and the popular Givens rotation based matrix parameterization.