Design of Discrete-time Matrix All-Pass Filters Using Subspace Nevanlinna Pick Interpolation
Paper and Code
Oct 25, 2022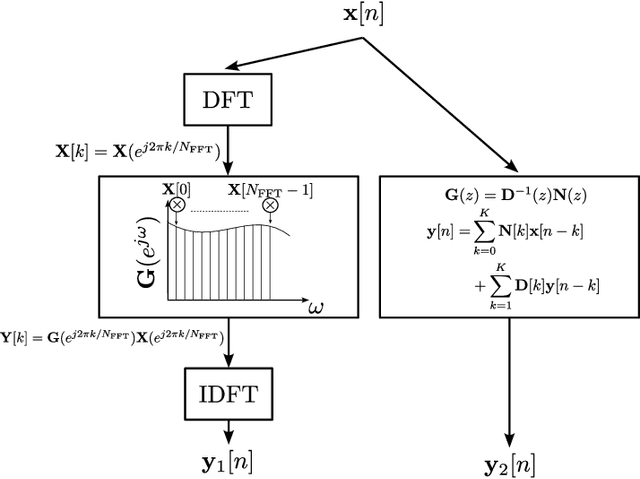

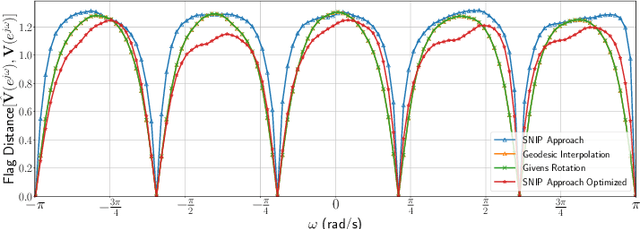

Unitary matrix-valued functions of frequency are matrix all-pass systems, since they preserve the norm of the input vector signals. Typically, such systems are represented and analyzed using their unitary-matrix valued frequency domain characteristics, although obtaining rational realizations for matrix all-pass systems enables compact representations and efficient implementations. However, an approach to obtain matrix all-pass filters that satisfy phase constraints at certain frequencies was hitherto unknown. In this paper, we present an interpolation strategy to obtain a rational matrix-valued transfer function from frequency domain constraints for discrete-time matrix all-pass systems. Using an extension of the Subspace Nevanlinna Pick Interpolation Problem (SNIP), we design a construction for discrete-time matrix all-pass systems that satisfy the desired phase characteristics. An innovation that enables this is the extension of the SNIP to the boundary case to obtain efficient time-domain implementations of matrix all-pass filters as matrix linear constant coefficient difference equations, facilitated by a rational (realizable) matrix transfer function. We also show that the derivative of matrix phase constraints, related to the group delay at the interpolating points, can be optimized to control the all-pass transfer matrices at the unspecified frequencies. Simulations show that the proposed technique for unitary matrix filter design performs as well as traditional DFT based interpolation approaches, including Geodesic interpolation and the popular Givens rotation based matrix parameterization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge