David W. Corne
Multi-objective evolutionary algorithms for quantum circuit discovery
Dec 11, 2018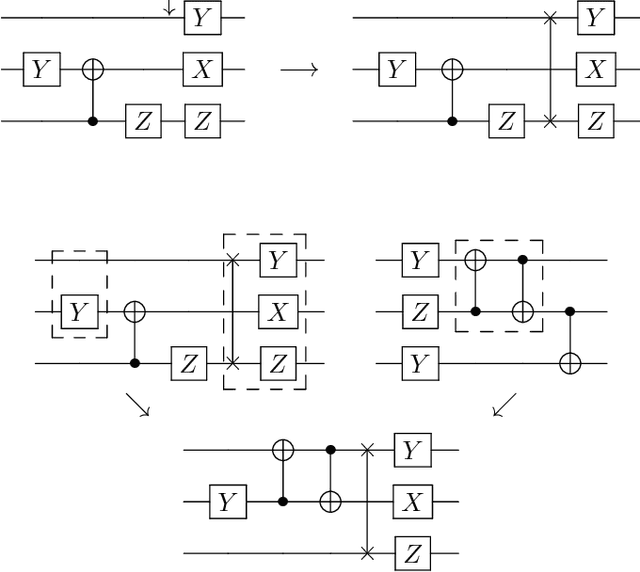
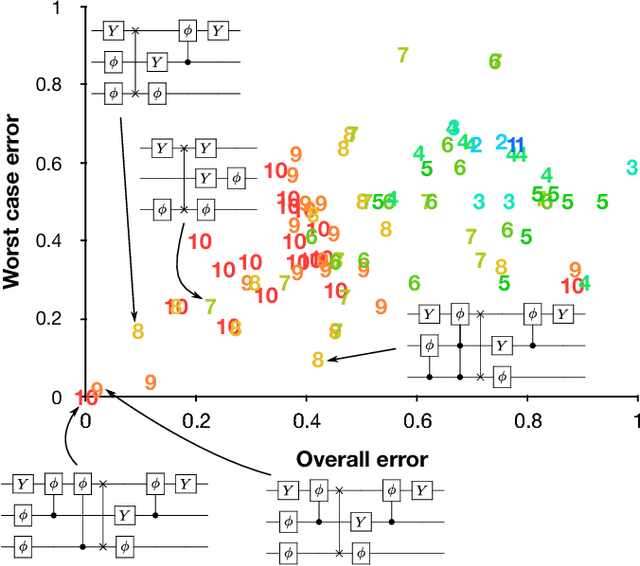
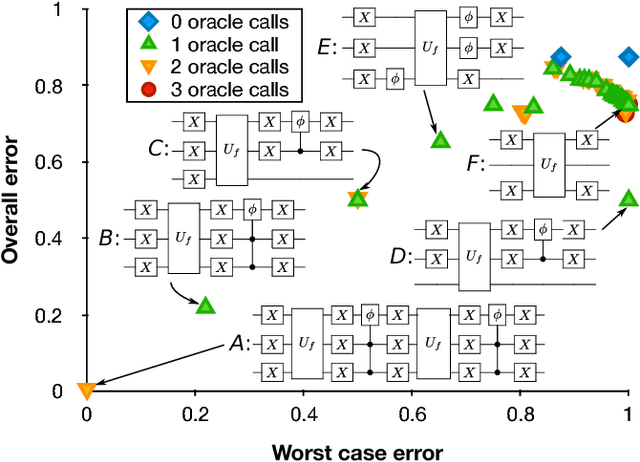
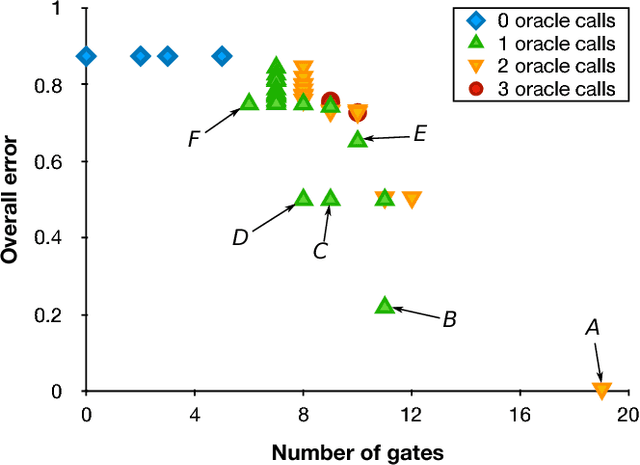
Abstract:Quantum hardware continues to advance, yet finding new quantum algorithms - quantum software - remains a challenge, with classically trained computer programmers having little intuition of how computational tasks may be performed in the quantum realm. As such, the idea of developing automated tools for algorithm development is even more appealing for quantum computing than for classical. Here we develop a robust, multi-objective evolutionary search strategy to design quantum circuits 'from scratch', by combining and parameterizing a task-generic library of quantum circuit elements. When applied to 'ab initio' design of quantum circuits for the input/output mapping requirements of the quantum Fourier transform and Grover's search algorithm, it finds textbook circuit designs, along with alternative structures that achieve the same functionality. Exploiting its multi-objective nature, the discovery algorithm can trade off performance measures such as accuracy, circuit width or depth, gate count, or implementability - a crucial requirement for first-generation quantum processors and applications.
Evolutionary Algorithms
May 28, 2018
Abstract:Evolutionary algorithms (EAs) are population-based metaheuristics, originally inspired by aspects of natural evolution. Modern varieties incorporate a broad mixture of search mechanisms, and tend to blend inspiration from nature with pragmatic engineering concerns; however, all EAs essentially operate by maintaining a population of potential solutions and in some way artificially 'evolving' that population over time. Particularly well-known categories of EAs include genetic algorithms (GAs), Genetic Programming (GP), and Evolution Strategies (ES). EAs have proven very successful in practical applications, particularly those requiring solutions to combinatorial problems. EAs are highly flexible and can be configured to address any optimization task, without the requirements for reformulation and/or simplification that would be needed for other techniques. However, this flexibility goes hand in hand with a cost: the tailoring of an EA's configuration and parameters, so as to provide robust performance for a given class of tasks, is often a complex and time-consuming process. This tailoring process is one of the many ongoing research areas associated with EAs.
Structural bias in population-based algorithms
Aug 22, 2014



Abstract:Challenging optimisation problems are abundant in all areas of science. Since the 1950s, scientists have developed ever-diversifying families of black box optimisation algorithms designed to address any optimisation problem, requiring only that quality of a candidate solution is calculated via a fitness function specific to the problem. For such algorithms to be successful, at least three properties are required: an effective informed sampling strategy, that guides generation of new candidates on the basis of fitnesses and locations of previously visited candidates; mechanisms to ensure efficiency, so that same candidates are not repeatedly visited; absence of structural bias, which, if present, would predispose the algorithm towards limiting its search to some regions of solution space. The first two of these properties have been extensively investigated, however the third is little understood. In this article we provide theoretical and empirical analyses that contribute to the understanding of structural bias. We prove a theorem concerning dynamics of population variance in the case of real-valued search spaces. This reveals how structural bias can manifest as non-uniform clustering of population over time. Theory predicts that structural bias is exacerbated with increasing population size and problem difficulty. These predictions reveal two previously unrecognised aspects of structural bias. Respectively, increasing population size, though ostensibly promoting diversity, will magnify any inherent structural bias, and effects of structural bias are more apparent when faced with difficult problems. Our theoretical result also suggests that two commonly used approaches to enhancing exploration, increasing population size and increasing disruptiveness of search operators, have quite distinct implications in terms of structural bias.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge