Centric selection: a way to tune the exploration/exploitation trade-off

In this paper, we study the exploration / exploitation trade-off in cellular genetic algorithms. We define a new selection scheme, the centric selection, which is tunable and allows controlling the selective pressure with a single parameter. The equilibrium model is used to study the influence of the centric selection on the selective pressure and a new model which takes into account problem dependent statistics and selective pressure in order to deal with the exploration / exploitation trade-off is proposed: the punctuated equilibria model. Performances on the quadratic assignment problem and NK-Landscapes put in evidence an optimal exploration / exploitation trade-off on both of the classes of problems. The punctuated equilibria model is used to explain these results.

On the Influence of Selection Operators on Performances in Cellular Genetic Algorithms

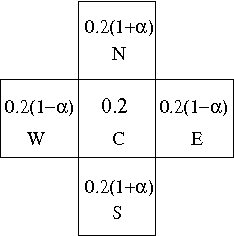
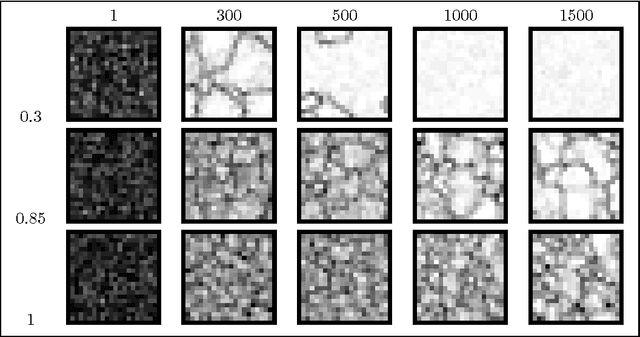
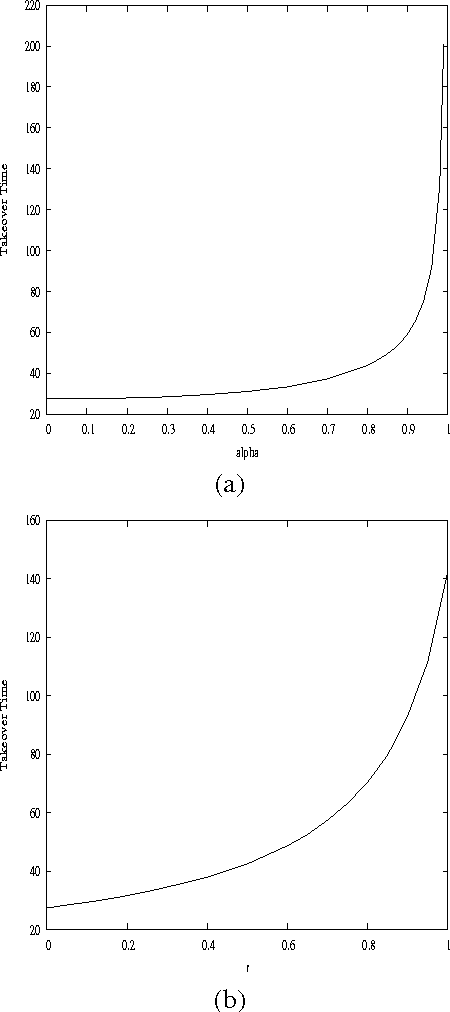
In this paper, we study the influence of the selective pressure on the performance of cellular genetic algorithms. Cellular genetic algorithms are genetic algorithms where the population is embedded on a toroidal grid. This structure makes the propagation of the best so far individual slow down, and allows to keep in the population potentially good solutions. We present two selective pressure reducing strategies in order to slow down even more the best solution propagation. We experiment these strategies on a hard optimization problem, the quadratic assignment problem, and we show that there is a value for of the control parameter for both which gives the best performance. This optimal value does not find explanation on only the selective pressure, measured either by take over time and diversity evolution. This study makes us conclude that we need other tools than the sole selective pressure measures to explain the performances of cellular genetic algorithms.

From Cells to Islands: An unified Model of Cellular Parallel Genetic Algorithms

This paper presents the Anisotropic selection scheme for cellular Genetic Algorithms (cGA). This new scheme allows to enhance diversity and to control the selective pressure which are two important issues in Genetic Algorithms, especially when trying to solve difficult optimization problems. Varying the anisotropic degree of selection allows swapping from a cellular to an island model of parallel genetic algorithm. Measures of performances and diversity have been performed on one well-known problem: the Quadratic Assignment Problem which is known to be difficult to optimize. Experiences show that, tuning the anisotropic degree, we can find the accurate trade-off between cGA and island models to optimize performances of parallel evolutionary algorithms. This trade-off can be interpreted as the suitable degree of migration among subpopulations in a parallel Genetic Algorithm.

Anisotropic selection in cellular genetic algorithms

In this paper we introduce a new selection scheme in cellular genetic algorithms (cGAs). Anisotropic Selection (AS) promotes diversity and allows accurate control of the selective pressure. First we compare this new scheme with the classical rectangular grid shapes solution according to the selective pressure: we can obtain the same takeover time with the two techniques although the spreading of the best individual is different. We then give experimental results that show to what extent AS promotes the emergence of niches that support low coupling and high cohesion. Finally, using a cGA with anisotropic selection on a Quadratic Assignment Problem we show the existence of an anisotropic optimal value for which the best average performance is observed. Further work will focus on the selective pressure self-adjustment ability provided by this new selection scheme.