On the Influence of Selection Operators on Performances in Cellular Genetic Algorithms
Paper and Code
Apr 05, 2008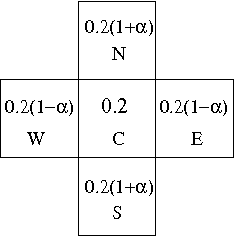
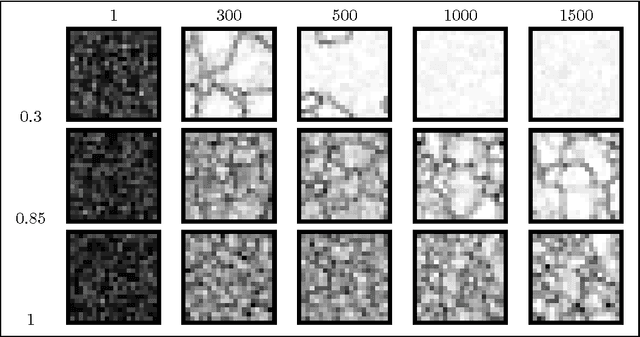

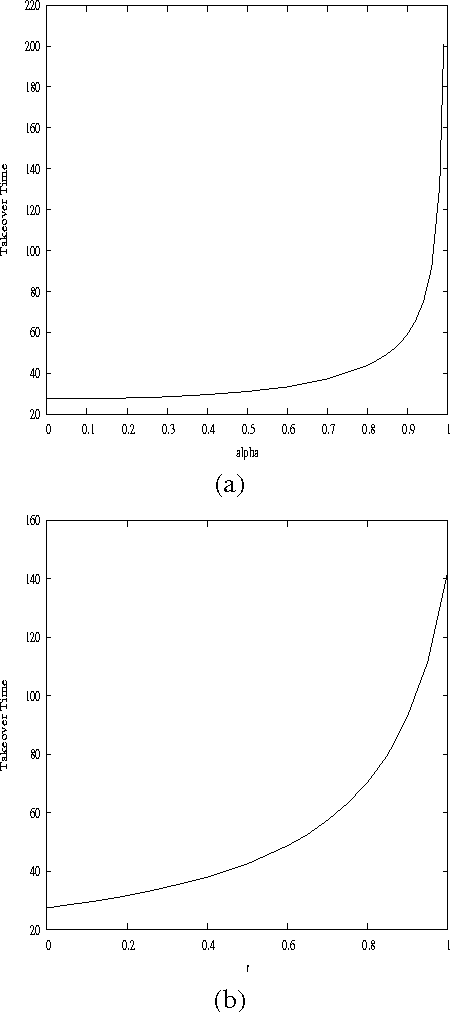
In this paper, we study the influence of the selective pressure on the performance of cellular genetic algorithms. Cellular genetic algorithms are genetic algorithms where the population is embedded on a toroidal grid. This structure makes the propagation of the best so far individual slow down, and allows to keep in the population potentially good solutions. We present two selective pressure reducing strategies in order to slow down even more the best solution propagation. We experiment these strategies on a hard optimization problem, the quadratic assignment problem, and we show that there is a value for of the control parameter for both which gives the best performance. This optimal value does not find explanation on only the selective pressure, measured either by take over time and diversity evolution. This study makes us conclude that we need other tools than the sole selective pressure measures to explain the performances of cellular genetic algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge